This is the first in a number of texts on the series of K7-sudoku plays that I have set myself as a task to produce this year in weekly editions, including thoughts on how it is they sound how they sound ánd reflections on combinatorial and other properties of the sudoku and related number grids as (durational) scores for alternating, interweaved multi-cut-ups of the two time-directions of a certain stretch of a recording kept on magnetic (K7)-tape.

25 min read 🤓

The Art of K7 :: Südokaising
[i] History _ Content _ Form

march 21, 2020

"break on through to the other side"

In the early days of the 'recorded music consumption boom' —roughly between the mid 1950s and the late 1970s, the period in which record companies and electronics industries made vinyl records and cassette tapes into products that pretty much every single Western individual from the age of, say, 12 on & upwards bought on a regular basis— pretty much all audio carriers came with an 'other side', access to which demanded a real —physical— rotation in space of the record or K7, on or in the playback device.

For magnetic tape, say K7s, that 'other side' is not the back side of the plastic carrier (which has its sound-saving magnetic emulsion on but one of its sides). The 'other side' is/are (a) different section(s) of the same side of the carrier. Turning a cassette tape in a cassette player reverses the direction of the tape's moving. Playback of the A-side rewinds the track on the B-side. Playback of the B-side rewinds the track on the A-side. Some types of cassette players come with an 'auto-reverse' option, which automatically reverses the playback direction, and starts playing the 'other side' once the end of the tape has been reached. Such players often include a button or a switch with which this reversing of the playback direction can be make to happen near to instantaneously, also during playback of the tape.

My 'sudoku K7 solution' technique is totally based on the availability of such a reverse switch on certain types of dictaphones, which allows for the continuous interlacing of fragments of two sound recordings that by chance found themselves on the same stretch of magnetic tape, with time running in opposite direction.

A detailed description of the serendipitous why and the when of my using (solved) sudoku grids as a 'temporal score' for this interlacing of K7 recordings can be found in the SoundBlog entry that I wrote around the time that I used it for the very first time, about fourteen years ago, performing live with Rinus van Alebeek at 'De Nor' in Heerlen (the Netherlands).

I executed and recorded quite a number of K7 sudoku's since then, always with a SONY TCM 500DV dictaphone, which for all of its lifetime was my favourite K7-instrument (and field recorder). At least partly due to my at —and with the passing of— times increaslingly rough and intense use, though, it died (that must've been some 6 or 7, maybe 8(?), years ago), beyond repair.

The (found and secondhand) dictaphones with a reverse play switch that I came across over the past few years were always far less versatile in use. They all missed the fluency of the playback direction switching that the SONY had, so were not really suitable for sudoku playing. It was only the end of last summer that WeiWei brought me one back from Taïwan that comes close: an Aiwa 'Crosstrainer' SP370 walkman/radio, in truly mint condition.

To well use this fine gift, on each of the 52 weekends of 2020 I will pick a K7 from my vast archive, and use it to record a K7-sudoku. Performed on the Aiwa, of course.

Throughout the year, I will collect them in a playlist on SoundCloud.

The "final results" of the project will later on be made available as digital download albums at Bandcamp's.

Serial dictaphony

The interlacing may feel random (and a bit further on in these 'sudoku writings' we will try to find why that is), but actually it is serial, in the sense that the durations of successive A- and B-plays (in undefined time-units, 'counts' or 'ticks'; they may be seconds, they may count less, or may be more) are read off from the 9 successive rows of a sudoku grid. Each row is a permutation of {1,2,3,4,5,6,7,8,9}, a series of nine durations, and nine of such permutations, as given by the successive rows of a sudoku grid, form a K7-sudoku's score, that as a player I then try to perform as correctly as I can: it's basic, it's simple, but indeed it is undeniably dictaphonic serialism, serial dictaphony ...😏...

It already at the time of its birth inspired a number of funny & interesting reflections, that, on this year's sudoku play-'Aiwa re-born' occasion, I will go and explore here in quite some detail.

As a thing for me to do, personally it is of course also a (loose?) referal back to my serial days, (in the 1980s as a student of Gottfried Michael Koenig, at the Utrecht institute of Sonology, and later, in the 1990s and early noughties, at Stockhausen's Kürten summer schools); and my subsequent, what I like to call serial détournements, recently for example in things like the SQWWO and Etude.

So. Then. Here we go again.

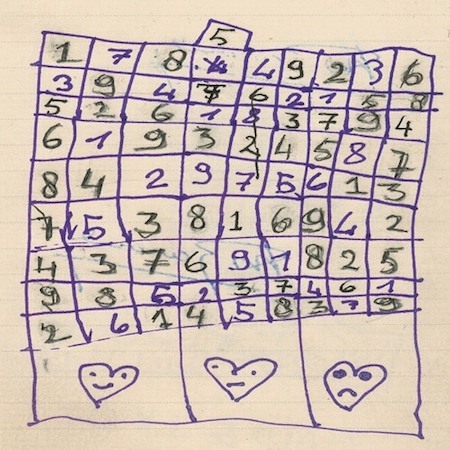For starters, you should know that I am not an amateur of solving sudoku puzzles, nor a specialist in sudoku math and/or design. It's these past couple of 'corona confinement' days only that I found myself looking ever more closely at how a bag full of occurrences of the first nine integers in a solved sudoku grid get spread out over 81 little squares. I ever filled in only a mere handful of sudoku puzzle grids myself. That must've been around the time that I first used them as a dictaphone score, in 2006, when my then nine-year old daughter drew for me the sudoku (picture above), that I then used in the 'De Nor' performance with Rinus. She also offered me a little booklet with sudoku puzzles, a few of its pages hand-decorated with the little plastic coloured sticky hearts that she got from her grandmother (we spent a few days of that year's Easter holidays in Maastricht) 🤓 .

It is not unlikely that for the 'sudoku plays' that I performed and recorded onward from that first time in 2006, until the demise of my SONY TCM 500DV, I always used one of these same grids.

And I used one of them again on September 29th 2019, at the very end of the "Do Not Interrupt Your Activity" event ( * ) at La Générale, for the very first live K7 sudoku that I did since many, many years, for which I picked the middle one from the picture above.

The DNIYA sudoku uses a 'Chroniqure Sonore' K7 recorded in 2001, shortly after the 9/11 that gave the new millennium its historical sudden bitter & unexpected twist. One side of the tape has the sound recorded from a CNN 9/11 broadcast { "Oh my God! The second tower is down..." }, on the other side there is the sound of a French speaking children's toy that I recorded at a friend's house { « Joue avec moi ... shoot avec moi ... » } [The 'shoot avec moi' is really curious, but it is what one hears the toy say, no?]

...

Form(alities), first

In theory, a sudoku K7-play is fully determined by the play's starting point on the cassette tape used, and the precise tempo of playing, i.e. the duration of a time unit, a count or tick. I never really fix a 'tempo' for a play beforehand, I just settle for one that seems appropriate, intuitively, depending on my mood, I guess, and on the kind of sounds and —probably— also the proper 'tempo' of the sound / music in the recording. Were the tempo fixed and the same for all plays, each of them would have the same duration: each sudoku play has 9 × 45 = 405 counts, and if a count lasts, say, one second, then a play, the derive across the tape, will take precisely six minutes and forty five seconds. In practice, though, the durations all differ. That's of course inherent to the 'live' playing and 'live' counting, which comes with mistakes and —it's unavoidable— temporal deviations, drifts and variations.

I re-performed the DNIYA sudoku as part of this year's weekly series, where it became number eight, Sudoku 202008.

---

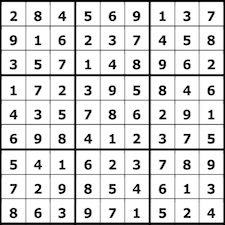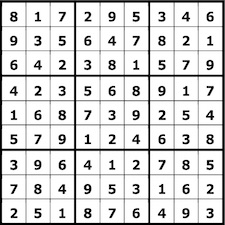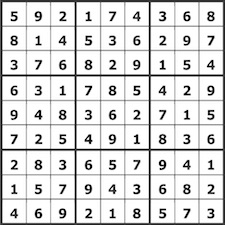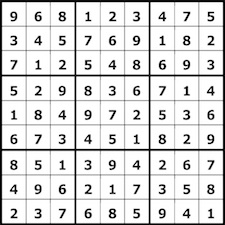The Sudoku grids used for the the first four 2020 Sudoku K7-plays

---

I will not continue to only use my handful of 'vintage' sudoku grids. Each of the 52 sudoku's planned for 2020, will get its own grid. That's not so difficult, as there are — no less, but also no more, than— 6,670,903,752,021,072,936,960, or, in plain english: [[ six sextillion six hundred and seventy quintillion nine hundred and three quadrillion seven hundred and fifty two trillion twenty one billion seventy two million nine hundred and thirty six thousand and nine hundred and sixty ]] different (completed) sudoku grids (about 6.671 × 10²¹)... (There will be a bit less —but still many, many more than a single human would be able to deal with in her lifetime— if we divide out all sorts of symmetries and transformations, that convert a given sudoku grid into others: rotations, reflections, applying a 1:9 permutation to the grid, exchanging blocks ... we will come back to this later.) ( ** )

This year then will give me an excuse to look into the properties of the grids, and think some more about the how's, why's and what's. How does, or: how does, a 'sudoko score' take a stretch a of cassette from 'here' to 'there'?

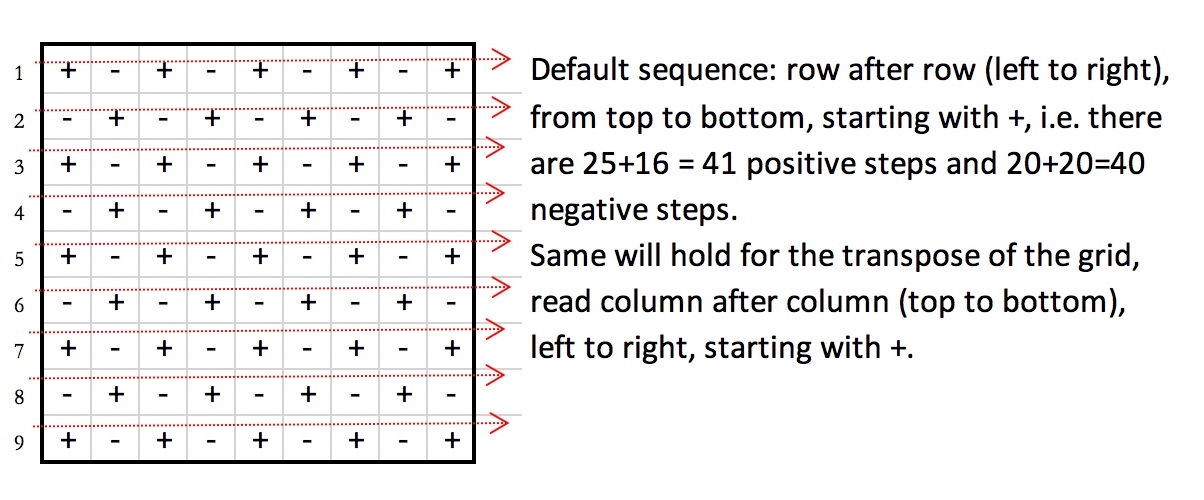
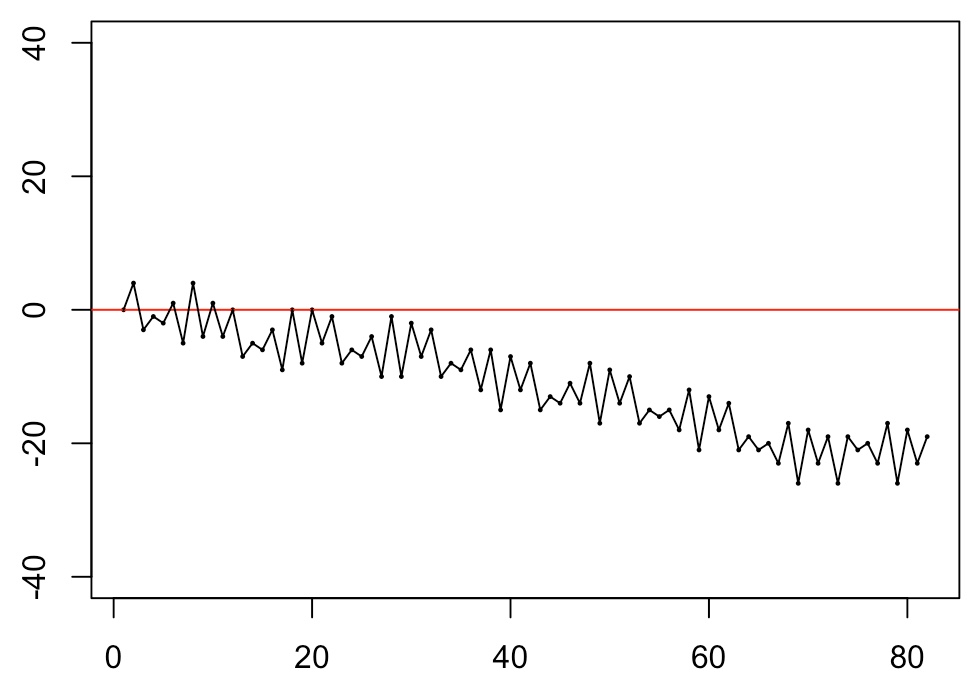
The following picture shows in minute detail how the playing of the K7's two (stereo) tracks evolves, visualising the alternation of the playback directions and durations, which cuts up (with repetitions) a certain stretch of (both of the tracks) and interlaces their playback. The visualisation is that for the third of this year's plays, Sudoku 202003.

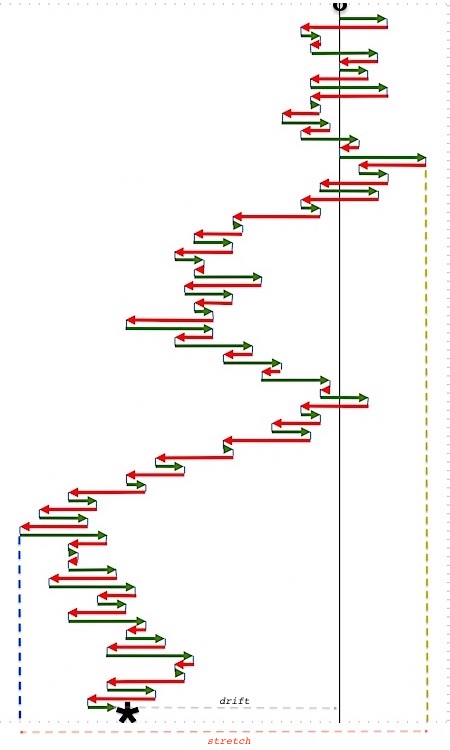The arrows show the alternate forward/backward playing of the K7 tape, starting from a given point zero; each next turn is activated by hitting the dictaphone's reverse switch, with the durations between successive hits (the duration of successive epochs, see below) given by the entries in the sudoku, read from the left to the right, row after row.

It's a sequence of durations, {s₁,s₂,...,s₈₀,s₈₁}, where the subsequence with (41) uneven indexes, s_2k-1 = {s₁,s₃,s₅...,s₈₁}, fixes the times of the 'forward plays', and the subsequence with (40) even indexes, s_2k = {s₂,s₄,s₆...,s₈₀}, fixes the times of the 'backward plays'.
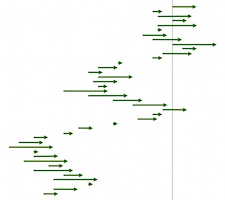
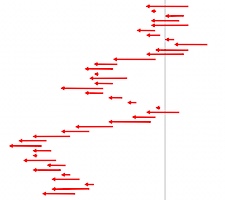
The uneven sequence is a 'multi cut-up' of one 'side' of a certain stretch of the K7 tape, and the even sequence is a 'multi cut-up' of the other 'side' of that same stretch. The uneven and even 'multi cut-up' are interlaced.

In the two pics below they have been separated:

{s1,s3,s5...,s81}	{-s2,-s4,-s6...,-s80}
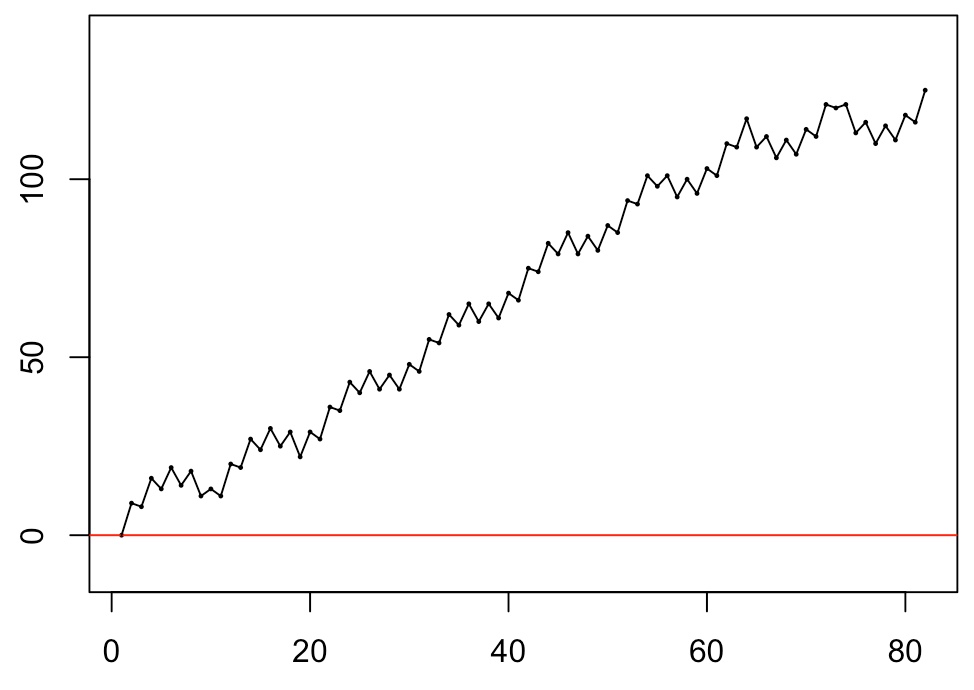
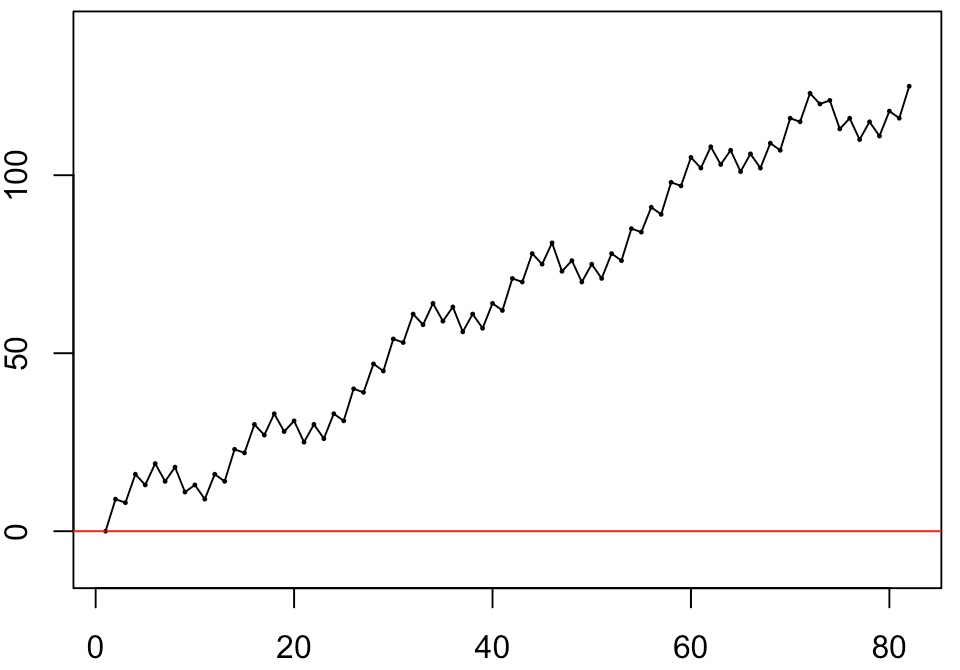
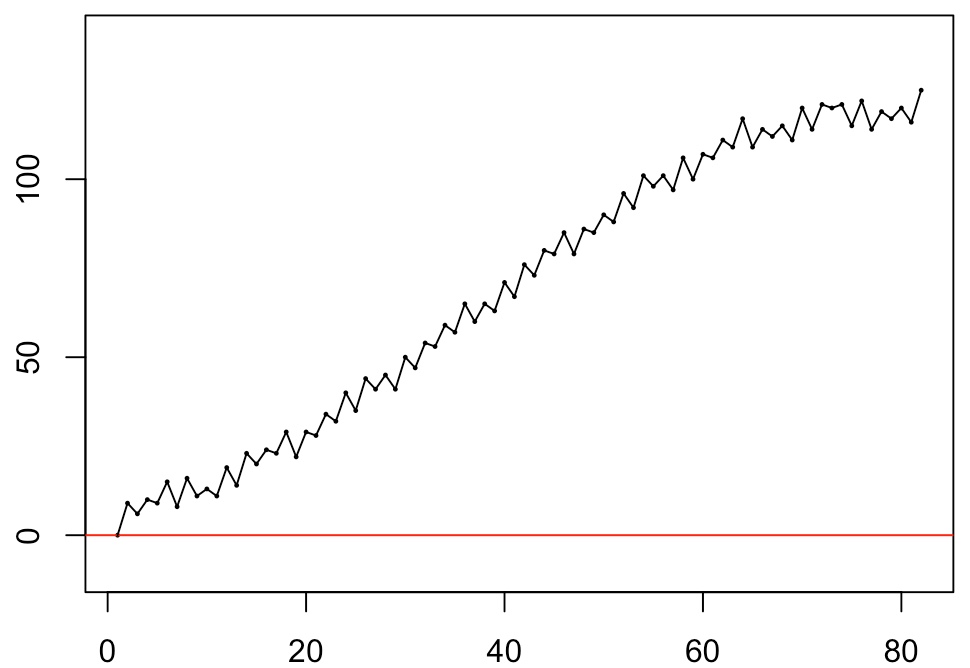
The negative signs in the even subsequence indicate that the tape's movement at these instances is in the reverse direction of that for the uneven subsequence. Interlacing —weaving— the two, we get the alternating sequence {sn} = {s1,-s2,...,-s80,s81}. The sequence of cumulative sums of this sequence indicates how far, at the end of each of the 81 durations, we have strayed from the zero point, either to the left (negative value) or to the right (positive value):

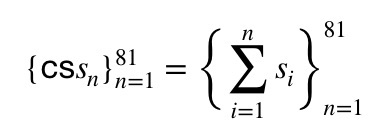The length of the K7-tape fragment that is covered by the sudoku play is equal to max{css_n} - min{css_n ∪ {0}} (the max here is always bigger than zero, because the first step is always a positive one). It obviously will vary from sudoku to sudoku, and we will name it the sudoku's stretch. It is the distance (in 'counts') between the blue-ish and the green-ish vertical dashed lines in the big picture above, and depends on how far to right and how far to the left of point zero the sudoku allows us to wander. The stretch of Sudoku 202003 is 33. The final term of the sequence of cumulative sums, css₈₁, indicates how far the sudoku play's end point, its finish, is away from the point zero where it started. We call it the drift of the sudoku. The drift of Sudoku 202003 is negative, it is -23.

These sort of simple reflections then in turn spark a number of questions, the answering of which will maybe want some smart combinatorial and counting arguments and/or (probably along with) brute computing force:

What is the maximal (positive) drift that a sudoku play can have (in number of counts), and what is the minimal (negative) drift?
Can all values between the min and the max occur as drift values? In particular, can a sudoku-play be 'flat', i.e. can it have a zero-drift, and in the end come back to where it started?
What is the largest stretch of tape that a sudoku play can cover?

On sudokaising text and lyrics

Apart from magnetic tape (and vinyl records) also the bulk of paper-printed texts has an 'other side' (indeeed, having an 'other side' is caracteristic for many analogue media!). It may be interesting to apply the 'sudokaising' technique to printed text pages, by making each side of the page a string of words, and then using the sudoku numbers either for word-counts or letter-counts two weave the two multi-cut up, like a K7-sudoku. (Of course, contrary to tape, the 'other side' of a page does not have an inverse timeline; so we'd need to choose to either to read the 'other side'-string backwards, or invert it prior to sudokaising.)

Such a textual cut-up is also realised in case the K7-recording we use has spoken or sung words, as the one used in the 11th of this year's sudoku-plays: it was a tape with on both sides a recording of Vicky reading Mosquitos.

That week's sudoko's drift was -95, with a stretch of 109, and here is, as an example, the text (__ the bastard's the master __) that was was produced by the 'sudokaising' (text from the one side is colored green, text from the other side is colored red):

It soon became one of my favourites as well
cut, all the same texture... He, he was
It soon became one o-exture
Soon became one of my fa- texture
He buttered his roll
Tuesday
tered his roll and ate

But Jeff was right about Tuesday
He was
He buttered his roll and ate
re-But
really slowly
But Jeff was right about
roll and ate
really slowly
Then he looked up
as well
lowly
Then he looked up again
and continue
I really think you
again an
I really think you
gain and continued his speech.
I thought this ni
You might even loathe lo
I thought this night tha
night that there was a burglar
sneaking around my room

You might not like all of it
was a burglar sneaking around my room,
yes! But it must've been
someway somewhere within Light
in my room, yes! But it must've been
someway somewhere within Light.
oom, yes! But it must've been
an animal, maybe a squi-can imagine
nimal, maybe a squirrel, or something
all in there, in

Pity, really! I was al
I was already looking forward to show
human, yeah
I was already looking forward to showing
that good-for-nothing of sound
nothing, what a cripple on crutches
is capable of...
like a body, pretty much encyclope
crutches
is capable of...
mm
like a bo

You see, there's all these pine-quencies, a gargantuan
there's all these pine-quen
trees, a gargan
there's all these pine-quen
trees in front of my window, yes?
some in fra
So I heard something climbing there,
up one of them
putting all of it down in minu
climbing there, up one of them
every single day
putting all of it down-ing there,
up one of them

But before that there was th-ustriously,
every single hour of every single day,
putting all of it down-ing there
up one of them
But befor-le hour of every single day,
putting
up one of them
But before that there was the soun-dustriously,
there was the sound of w
industriously, every
that, there was the sound of water running.

And I sai-twenty-five
said to myself, Heinrich, I said,
the bastard's the master,
said, the bastard
He has been working on it for over twenty
I said to myself, Heinrich
has been work
Heinrich, I said, the bastard's down there,
collecting his
wrapped up by now, the master,
the bastard's down there, collect
wrapped up by no
collecting his courage by drink
should have it all wrapped up by now, the master,
bastard's down there, collecting his
wrapped up by now, the master,
the bastard's down there, collecting his courage
by drinking a beer.

And he should have it
courage by drinking
And he should have it all wrapped up by now,
the master.

Form(alities), second: the random walkers' drift
rand(9) ← perm(9) ← lasq(9) ← sudoku

A sudoku play is like a random walk. Random walks are pretty intriguing mathematical objects. Sudoku plays are not really random walks, though. They have the walker alternately make steps to the left and to the right, each with some 'length', between 1 and 9, but the successive step lengths are not randomly picked. The lengths of the steps that are made during a play are not 'independent' from one another.

rand(9)-play's drift

Still, each sudoku grid is of course also one of the possible rand(9)-grid (i.e. a grid where each of the 81 cells is a random integer between 1 and 9, picked uniformly, say, so that each number shows up with a probability of 1/9).
(Chances of randomy producing a sudoku grid, though, are pretty slim: *** )

Like sudoku grids, we can use a rand(9)-grid to define alternate steps to the right and the left, this time each with a random length, between 1 and 9. And this indeed is (a little variation on) a random walk: it is an alternating sequence of the 81 independent and identically distributed random variables: X₁, -X₂, X₃, -X₄, ... , -X₈₀, X₈₁. Each variable's values are those of the cast of a fair 9-sided dice, with expected value E[X] = 5, and variance Var(X) = 6.667. Like a Suduko play, also each rand(9)-play has a drift, which in this case is the sum of 81 iid random variables, hence E[driftrand9] = E[X₁] - E[X₂] + E[X₃] - E[X₄] + ... - E[X₈₀] + E[X₈₁] = 5 and (by independence) Var[driftrand9] = Var[X₁] + Var[X₂] + Var[X₃] + Var[X₄] + ... + Var[X₈₀] + Var[X₈₁] = 81 × 6.667 ≈ 540.

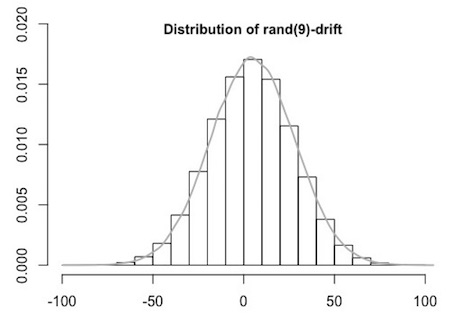
The max and min drifts of rand(9)-plays are easily calculated, and are (strict) bounds for the possible drift of sudoku-plays. The max drift of rand(9)-play is that of a sequence where all 41 uneven indexed terms are equal to 9, and all 40 even indexed ones are equal to 1: it is + 329. And the min drift sequence has all uneven indexed terms equal to 1 and all even indexed ones equal to 9, making for a drift of 41 - 360 = - 319. (In the math theory of random walks the indices are often called 'epochs'. I like that, so in what follows I will use 'epoch' for index: each of the steps in a random walk occurs at a given epoch.) The grids realising these extreme drifts obviously are unique (each occurring with a dazzlingly small probability of 1 in 9⁸¹) and, obviously, are not sudoku plays.

The central limit theorem learns that the values of rand(9)-drifts should be (approximately) normally distributed, with mean 5 and variance 540: about 68% of the rand(9)-drifts are roughly between -18 and 28. This is confirmed by the following histogram made in R of the drift-values of 200,000 rand(9)-plays. The mean drift was 4.917, the variance 539.79, the max 99 and the min -94:

perm(9) ← lasq(9)

In the space of rand(9)-grids, the move towards sudoku-grids is one of increasing order (decereasing entropy). As a first step, let's consider the grids where rows are no longer randomly filled, but asked to be permutations of the sequence 1:9. That decreases the number of possible grids from about 2 × 10⁷⁷ to 9!⁹, which is around 10⁵⁰. It is easy to determine the max and min drift of a perm(9)-play: we need to assure that the high values go to the terms at uneven epochs, and the low values go to the terms at even epochs. That means that in the positive direction we will have 5 × (9+8+7+6+5) = 175 and 4 × (9+8+7+6) = 120, hence the max possible drift of a perm(9)-play will be 590 - 405 = + 185. And a similar counting shows the min possible drift of a perm(9)-play to be - 175.

Whereas the max/min drift rand(9)-plays were unique, in the set of perm(9)-plays they are abundant: there are (5!×4!)⁹ possible max and just as many min drift perm(9)-plays.

perm(9)-play's drift

If we continue to look at the grid as a sequence of length 81, in a perm(9)-grid we have lost independence in the picking of the term's values. But we do have independence in the choice of the successive nine permutations that make up the grid. The drift of a perm(9)-play's is the sum of an alternating sequence of 9 independent and identically distributed random variables, each of which takes values in the possible drifts of a single permutation: X₁ - X₂ + X₃ - X₄ + X₅ - X₆ + X₇ - X₈ + X₉.
For each of the uneven rows of the grid, the drift is the difference between a sum made up of 5 of the 9 terms in the permutation, minus a sum made up of 4 of the remaining ones. For each of the even rows, the drift is the difference between a sum made up of 4 of the rows of the 9 terms, minus a sum made up of the 5 remaining ones. That is, the possible drifts of an even row are obtained by negating those of an uneven row, and vice versa. To find the possible drifts, we just need to determine all the possible sums that can be obtained from the distinct quintuples and the distinct quadruples picked from the sequence 1:9. There are '9 choose 5' = 126 of such quintuples and '9 choose 4' = 126 of such quadruples. (And we can simply disregard the order in which the sums are made :-) /\//)
The possible sums are indicated in the following barplot, where the bars are proportional to their frequencies:

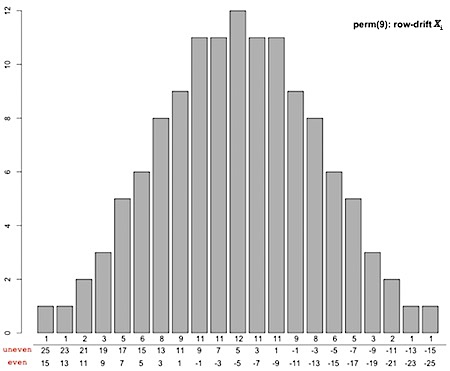(The leftmost and rightmost numbers show once again that the max and the min possible drifts of a perm(9)-play will be 5 × 25 + 4 × 15 = 185 and 5 × -15 + 4 × -25 = -175, each of the sums obtainable in just one way, realised by 5! × 4! of the total 9! permutations.)

This also shows that the drift of a perm(9), a permutation of 1:9, is always uneven, hence the drift of any perm(9)-play will be uneven. As any sudoku play is also a perm(9)-play, also the drift of a sudoku-play is always uneven. There are, in particular, no 'flat' sudoku-plays, i.e. sudoku-plays with drift = 0 do not exist: a sudoku-play will never return to the precise spot on the tape from where it started.

It is clear from the picture that, for each i, E[X_i] = 5, and by straightforward calculation we find Var(X_i) = 66.667, whence E[driftperm9] = 5 and (by independence) Var(driftperm9) = 9 × Var(X_i) = 600.

Here is a histogram made in R of the drift-values of 200,000 perm(9)-plays; the mean drift was 4.097, the variance 600.31, the max 111 and the min -95:

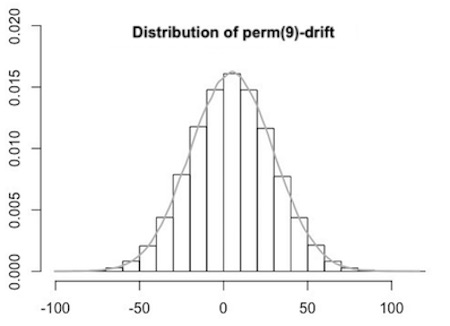These little perm(9)-play calculations bring the max drift of a sudoku play down to, actually, strictly less than 185 and the min drift to strictly more than -175, as one quickly finds that in a max/min drift perm(9)-grid it is impossible 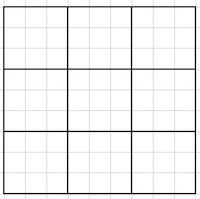to also have all columns be permutations: a max/min drift perm(9)-grid can not be a 9x9 latin square (a grid in which both rows and columns are permutations; let's here call it a lasq(9)-grid), and hence it cannot be a sudoku-grid, because a sudoku-grid is a lasq(9)-grid with the additional restriction that also the nine 3x3 blocks of cells (drawn starting from the top-left cell) are permutations. ( **** )

cyclic lasq(9)-grids

Uniform random generation of latin squares of size 9 (and a fortiori, of sudoku grids) is far less evident than that of the rand(9)- and perm(9)-grids ( ***** ), and I'll have to continue to think about whether there is a smart way to get an idea of the distribution of sudoku plays' drift values other than by calculating lots of them. Well, the expected values in both cases will remain 5, as both the set of lasq(9)-grids and that of sudoku-grids just feel to be seated 'symmetrically' in the space of rand(9)-grids and perm(9)-grids... with an increasing dependence between entries in the grid, as we crawl up to sudoku space :-) ...

...

rand(9) ⊃ ^{perm(9) ⊃ lasq(9) ⊃ sudoku}

...

There is an easy way though to generate a particular set of latin squares, and then make these into sudoku's, conserving the value of the grid's drift. I don't know whether these were given a name already elsewhere by people that studied latin squares and sudoku design, but I call them cyclic, as you make them by picking a permutation of 1:9 for the first row or column, and then 'cycle through it' in successive steps for the eight remaining rows or columns. Here is an example. We start with (4, 7, 2, 1, 3, 6, 9, 8, 5) (the generating permutation) in the first row, and then 'cycle' the permutation over 'to the right':

As the square is completely determined by its 'generating' permutation, we find that we can directly calculate the drift of such a 'cyclic' play from the initial permutation. If that permutation is (s₁,s₂, ... ,s₉), then the drift is 9s₁ - 7s₂ + 5s₃ - 3s₄ + s₅ + s₆ - 3s₇ + 5s₈ - 7s₉.
The example's drift is -19.

From this 'lasq(9) drift' formula it is easy to find that the max and min drift values for this highly regular type of latin square are 125 and -115 respectively, and that there are precisely 16 max grids and 16 min grids realising these 'extreme' drifts.

I let R determine the drift values for the full set of 9! 'cyclic latin squares' (one for each permutation of 1:9). As expected by symmetry, the mean and median both are equal to 5. We already found the min and the max. The variance added up to a dazzling 1866.667 🤓 ...
Here's a picture...

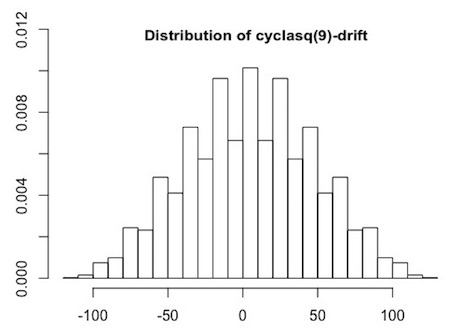The cyclasq(9)-drift values appear to form an arithmetic sequence with first term -115, common difference 4 and last term 125; in particular, as we already knew, all drifts are uneven

cyclic lasq(9)-grids ← cyclic sudoku-grids

There is an awful lot of symmetry, in all of these grid sets. If one reflects a 9 × 9 grid horizontally (column 5 is the axis), vertically (row 5 is the axis), or in either of the two diagonals (reflection in main diagonal (1,1):(9:9) is usually called transposition), a latin square remains a latin square, a sudoku remains a sudoku, and also the corresponding play's drift is conserved. That is because all of these transformations map uneven (row/column)indexes to uneven (row/column)indexes, whence also the epochs in the vectorised grid keep their parity. The same holds for rotation of the grid. These transformations together are all the symmetries of a square, they form the dihedral group of order 8. These symmetries preserve latin squareness, sudoku-ness and drift value.

Permuting the rows and/or permuting the columns of a latin square preserves the property of being a latin square, but in general it will not preserve the property of being a sudoku, nor the value of the corresponding play's drift. (It will conserve drift in case the permutation does not change the parity of the indexes, i.e. it should send (un)even columns/rows to (un)even columns/rows.) Some permutations will always convert a cyclic lasq(9)-grids into a sudoku, which provides an easy way to generate (a relatively small number of) sudoku's. In particular (1, 4, 7, 2, 5, 8, 3, 6, 9) does so, whenever applied to the rows or the columns of a cyclic lasq(9)-grid. (It is like cycling a permutation in triplets; we might call it '3-sliding'; in Dutch I named it a 'drieschuiver'). It gives us a couple of sets of highly structured sudoku's, say, the cyclic sudoku's, with a drift-distribution that is the same as that of the cyclic latin squares.

Here is an example:

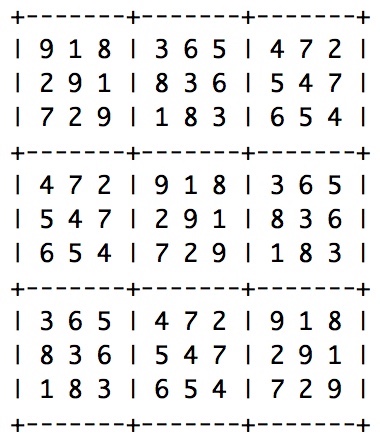This ↑ is one of the 16 cyclic latin squares that have a max drift-value of 125.
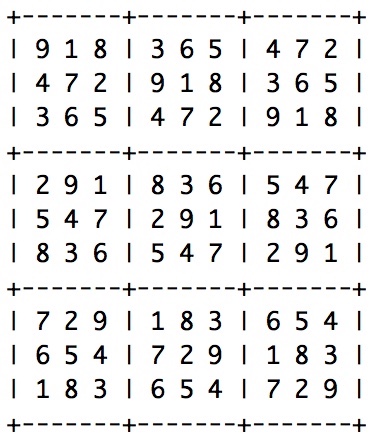This ↑ is the cyclic sudoku obtained by 3-gliding the rows of the above max drift latin square. The drift of course remains 125.
This ↑ is the cyclic sudoku obtained by 3-gliding the columns of the above max drift latin square. The drift of course remains 125.

—next read on my Sudoku Solutions:—The Art of K7 :: Südokaising [ii]

notes __ ::
(*) The one long single afternoon show "Do Not Interrupt Your Activity" was curated and co-organised by « L'Espace P()tentiel », the Brussels-based art-curating & -theorising duo Raya Lindberg & Nadège Derderian. [ ^ ]
(**) Felgenhauer, Bertram & Jarvis, Frazer. (2005). Enumerating possible Sudoku grids. [ ^ ]
(***) There are 9⁸¹ rand(9)-grids, making the probability that a rand(9)-grid happens to be a sudoku-grid about equal to (6.671 × 10²¹)/9⁸¹ ≈ 3.4 × 10^-56... pretty much zero, that is. [ ^ ]
(****) There are 5,524,751,496,156,892,842,531,225,600 lasq(9)-grids (about 5.525 × 10²⁷, making the probability that a lasq(9)-grid happens to be a sudoku-grid equal to about (6.671 × 10²¹)/(5.525 × 10²⁷⁾ ≈ 1.2 × 10^-6... indeed, lasq(9)-grids're getting a bit closer. A tiny bit... [ ^ ]
(*****) Fontana, Roberto. Random Latin squares and Sudoku designs generation. Electron. J. Statist. 8 (2014), no. 1, 883--893. doi:10.1214/14-EJS913. [ ^ ]

Follow @soundblog

tags: k7, sudoku, combinatorics

# .496.