SoundBlog ♫ "Yes, I am a Sudokist!"

This text provides the ins and outs of a new series of (instrumental) pieces of music from sudoku solutions. It starts with ‘_to Yoko Miura’, a suite for four toy piano's and electronics (or a vintage electronic organ).
The second is ‘27 latin variations on a Sudoku Solution for Perished Piano', immediately followed by a third: ‘22 sudoku variations on a Sudoku Solution for Perished Piano'. When you play the 49 variations, listen carefully: this is a profound and undeniably solipsist music, played by a piano that like a phantom, a ghost awakened, comes singing to you from a distant, unreachable world.

[ quicknav-: Neoplasticity | 4 Toy Pianos | sequencing | 27 latin variations | 22 sudoku variations ]

22 min read 🤓

Uit de kast: "Yes, I am a Sudokist!" 😏

17 july - 4 october, 2024

«.« Longtemps, je me suis douché de bonne heure,
à la recherche du sens perdu... ».»

[ quicknav-: Neoplasticity | 4 Toy Pianos | sequencing | 27 latin variations | 22 sudoku variations ]

My use of sudoku solutions as directives for musical performance and/or composition (sometimes in a rather loose and other times in a pretty strict sense) goes back to a duo cassetteurs performance in the Dutch city of Heerlen with Rinus van Alebeek, at the time of this writing eightteen years back in time, on April 14th 2006, where I decided that I would use the numbers in the grid of a sudoku solution to tell me how many counts (beats) to mentally make, before using the auto reverse button of my Sony TCM 500DV dictaphone to change the play direction of the cassette.

A detailed technical discussion and description of that sort of 'südokaising' can be found in an earlier post, from 2020, when I produced one K7 sudokaising track for every week of the year, to make good use of another walkman cassette player with an auto-reverse switch that I then recently had found, and which allowed me tp finally make up for the loss of the wonderful little Sony machine that I originally used for the südokaising, but that had stopped functioning already many years before. A selection of the sounding results of this sudoku-solution-determined switching of play direction (time folds) together form the first three digital albums with 'music from sudoku solutions', available on Bandcamp.

From the very sudoku start I often explained that the use of such number grids, enabled me to perform on the dictaphone in a serialist way. And of course it is only one little step from there to actually begin and take the numbers kind of as the number series that were used by a whole range of 20th century composers in realising their—more or less— strict serial composition work. In case these number series are the ones found in a sudoku solution, well, then of course the composition technique would better no longer be called serialist, but sudokist. That's how and why in a second long text on my 'südokaising', I introduced the term sudoskism.

"Südo, kiss me!" is the first piece-'thing' in which I use sudoku solutions in a totally straightforward manner to (indeed:) generate a musical composition; for lack of other and better terms, you may call it a 'music formula', or a 'meta-composition'. Short of actually being an algorithm, it is algorithmic at heart; which you will find to be applicable to most strictly sudoko solutions-led pieces.

Neoplasticity

"Südo, kiss me!" uses six sudoku solutions to generate an electronic 'chant' of six voices, one soduku solution per voice. Each voice starts from some chosen base note, and then uses the numbers in the sudoku solutions (reading, top to bottom, column after column, left to right) to alternatingly go up, then down, up, down, et cetera that number of half notes. The relative durations are given by the numbers in the same sudoku solution (read, left to right, row after row, from top to bottom). Thus, say, the first voice uses the following sudoku solution :

If that voice's base note is E(4), then the first four notes of the piece will be : (E(4) + 9 =) Cis(5) (-5 =) As(4) (+4 =) C(5) (-8 =) E4, with respective durations 9, 6, 2 and 4 'ticks'. The duration of each "Sudo, kiss me!" then is 9 × 45 = 405 'ticks'. In the "Sudo, Kiss Me!" version that is available on Bandcamp, a tick lasts 12 seconds, hence the duration of one "Sudo, Kiss Me!" part is precisely 81 minutes. The voices, defined as lists of midi-note numbers, are then played by Sonic Pi's ':beep' synth (basically is a pure sine wave). The result is aesthetically highly pleasing, its unrelenting step-geometry has a strange yet super-soothing attraction 😇. In its sonic purity and its unflappable unfolding of the set of perfectly balanced distributions of the nine digits, in time lengths and the sizes of successive intervals, it is like an abstract choral of tinniti tones that encapsulates my own (moderate form of) tinnitus, which becomes like the unending organ tone around which "Südo, kiss me!" evolves. The structure and sounds of the piece are, by sheer coincidence, a pure and almost literal embodiment of Dutch ultramodern neoplastic painter Piet Mondrian's concept of 'neoplastic music' (in his Dutch essay on "The 'Bruiteurs Futuristes Italiens' and 'the' new in music", published in De Stijl, volume 4 no. 8 and 9, 1921).

_to: Yoko Miura. Sudoku Solutions for Four Toy Piano's & Electronics

This series of pieces for Four Toy Piano's and Electronics (or, whenever performed live, four toy piano's and vintage electronic organ) came into being over the first half of 2024, and is—obviously 😇— dedicated to our Japanese friend musician Yoko Miura, who has been so masterfully improvising on Rébus' and other's Michelsonne toy piano, with us and without us, for many, many years, during her yearly concert tours of Europe. Each of the compos uses a single sudoku solution to determine the notes and their durations for the four toy piano voices. The nine numbers are interpret as the notes in a nine tone scales.
Pieces 1, 3, 6 and 7 use the C and B nine tone scales, placed on the Michelsonne toy piano as in the following pictures.

C nine tone scale, C(3)-D-Es-E-Fis-G-Gis-A-B

B nine tone scale, B(3)-Cis-D-Es-F-Fis-G-Gis-Ais

Here is the sudoku solution used for the first piece (“1. beginning, strict and allegretto”), followed by a detailed description of how the number matrix is interpreted as a toy piano quartet:

The first toy piano voice has as its list of notes the sequence of rows in the sudoku, read from top to bottom, and each row from left to right: 9, 3, 4, 1, 6, 7, 8, 5, 2, 2, 8, 5, 9, 3, 4, 1, 6, 7, 7, 1, 6, 2, 8, 5, 9, 3, 4, 4, 9, 3, 7, 1, 6, 2, 8, 5, 5, 2, 8, 4, 9, 3, 7, 1, 6, 6, 7, 1, 5, 2, 8, 4, 9, 3, 3, 4, 9, 6, 7, 1, 5, 2, 8, 8, 5, 2, 3, 4, 9, 6, 7, 1, 1, 6, 7, 8, 5, 2, 3, 4, 9, and interpreted as the notes in the C nine tone scale, numbered as 1=C(3), 2=D, 3=Es, 4=E, 5=Fis, 6=G, 7=Gis, 8=A, 9=B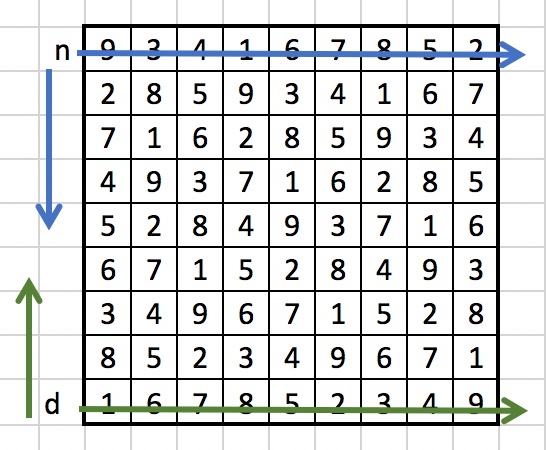

The durations for this sequence of notes are given by the sequence of rows, read from bottom to top, and each row read from left to right: 1, 6, 7, 8, 5, 2, 3, 4, 9, 8, 5, 2, 3, 4, 9, 6, 7, 1, 3, 4, 9, 6, 7, 1, 5, 2, 8, 6, 7, 1, 5, 2, 8, 4, 9, 3, 5, 2, 8, 4, 9, 3, 7, 1, 6, 4, 9, 3, 7, 1, 6, 2, 8, 5, 7, 1, 6, 2, 8, 5, 9, 3, 4, 2, 8, 5, 9, 3, 4, 1, 6, 7, 9, 3, 4, 1, 6, 7, 8, 5, 2

The second toy piano voice has as its list of notes the sequence of rows in the sudoku, read from bottom to top, and each row from right to left: 9, 4, 3, 2, 5, 8, 7, 6, 1, 1, 7, 6, 9, 4, 3, 2, 5, 8, 8, 2, 5, 1, 7, 6, 9, 4, 3, 3, 9, 4, 8, 2, 5, 1, 7, 6, 6, 1, 7, 3, 9, 4, 8, 2, 5, 5, 8, 2, 6, 1, 7, 3, 9, 4, 4, 3, 9, 5, 8, 2, 6, 1, 7, 7, 6, 1, 4, 3, 9, 5, 8, 2, 2, 5, 8, 7, 6, 1, 4, 3, 9, and interpreted as the notes in the B nine tone scale, 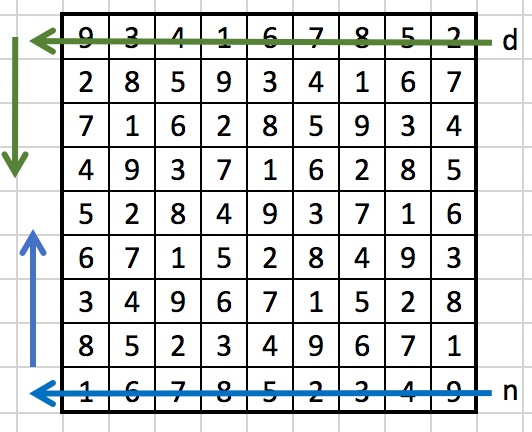numbered as 1=B(3), 2=Cis, 3=D, 4=Es, 5=G, 6=Fis, 7=G, 8=Gis, 9=Ais.

The durations for this sequence of notes are given by the sequence of rows, read from top to bottom, and each row read from right to left: 2, 5, 8, 7, 6, 1, 4, 3, 9, 7, 6, 1, 4, 3, 9, 5, 8, 2, 4, 3, 9, 5, 8, 2, 6, 1, 7, 5, 8, 2, 6, 1, 7, 3, 9, 4, 6, 1, 7, 3, 9, 4, 8, 2, 5, 3, 9, 4, 8, 2, 5, 1, 7, 6, 8, 2, 5, 1, 7, 6, 9, 4, 3, 1, 7, 6, 9, 4, 3, 2, 5, 8, 9, 4, 3, 2, 5, 8, 7, 6, 1

Note that this second voice sequence is the retrograde of the first voice notes sequence: it reverses the order of the note numbers and the corresponding duration numbers. As it is played in the B nine tone scale, the result is a transposition of the retrograde of the first voice.

The third and fourth toy piano voice then use the transposition of the matrix, or, eqivalently, for these two voices we read the original sudoku colunm-wise, in vertical direction. The third toy piano voice has as its list of notes the sequence of columns in the sudoku, read from left to right, and each column from top to bottom: 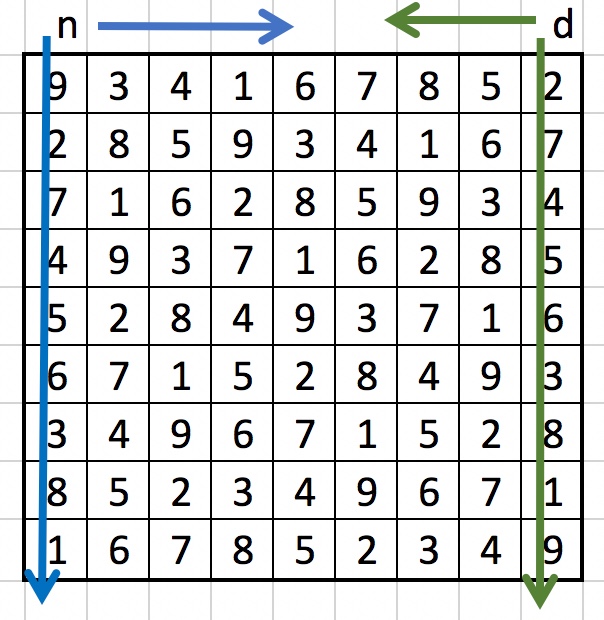9, 2, 7, 4, 5, 6, 3, 8, 1, 3, 8, 1, 9, 2, 7, 4, 5, 6, 4, 5, 6, 3, 8, 1, 9, 2, 7, 1, 9, 2, 7, 4, 5, 6, 3, 8, 6, 3, 8, 1, 9, 2, 7, 4, 5, 7, 4, 5, 6, 3, 8, 1, 9, 2, 8, 1, 9, 2, 7, 4, 5, 6, 3, 5, 6, 3, 8, 1, 9, 2, 7, 4, 2, 7, 4, 5, 6, 3, 8, 1, 9, also interpreted as the notes in the B nine tone scale

The durations for this sequence of notes are given by the sequence of columns, read from right to left, and each coliumn read from top to bottom: 2, 7, 4, 5, 6, 3, 8, 1, 9, 5, 6, 3, 8, 1, 9, 2, 7, 4, 8, 1, 9, 2, 7, 4, 5, 6, 3, 7, 4, 5, 6, 3, 8, 1, 9, 2, 6, 3, 8, 1, 9, 2, 7, 4, 5, 1, 9, 2, 7, 4, 5, 6, 3, 8, 4, 5, 6, 3, 8, 1, 9, 2, 7, 3, 8, 1, 9, 2, 7, 4, 5, 6, 9, 2, 7, 4, 5, 6, 3, 8, 1

The fourth toy piano voice has as its list of notes the sequence of columns in the sudoku, read from right to left, and each column from bottom to top: 9, 1, 8, 3, 6, 5, 4, 7, 2, 4, 7, 2, 9, 1, 8, 3, 6, 5, 3, 6, 5, 4, 7, 2, 9, 1, 8, 2, 9, 1, 8, 3, 6, 5, 4, 7, 5, 4, 7, 2, 9, 1, 8, 3, 6, 8, 3, 6, 5, 4, 7, 2, 9, 1, 7, 2, 9, 1, 8, 3, 6, 5, 4, 6, 5, 4, 7, 2, 9, 1, 8, 3, 1, 8, 3, 6, 5, 4, 7, 2, 9, and interpreted as the notes in the C nine tone scale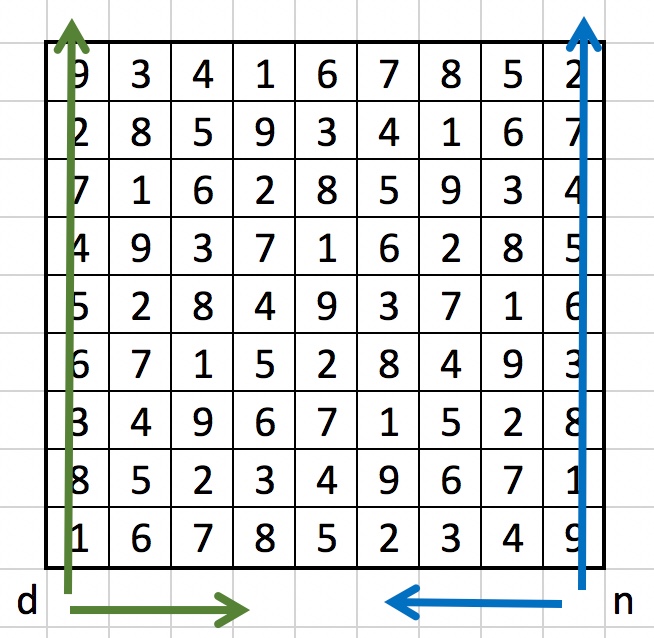

The durations for this sequence of notes are given by the sequence of columns, read from left to right, and each coliumn read from bottom to top: 1, 8, 3, 6, 5, 4, 7, 2, 9, 6, 5, 4, 7, 2, 9, 1, 8, 3, 7, 2, 9, 1, 8, 3, 6, 5, 4, 8, 3, 6, 5, 4, 7, 2, 9, 1, 5, 4, 7, 2, 9, 1, 8, 3, 6, 2, 9, 1, 8, 3, 6, 5, 4, 7, 3, 6, 5, 4, 7, 2, 9, 1, 8, 4, 7, 2, 9, 1, 8, 3, 6, 5, 9, 1, 8, 3, 6, 5, 4, 7, 2

The fourth voice is a transposition of the retrograde of the third voice.

The sudoku solution used for this first toy piano quartet, as you may verify, is a somewhat special one, with a lot of 'symmetry' and 'repetitions'. It is what I call a 'cyclic sudoku solution' and generated from a 'cyclic latin square' (with maximal drift), as you will find explained in some detail in my first text on südokaising.

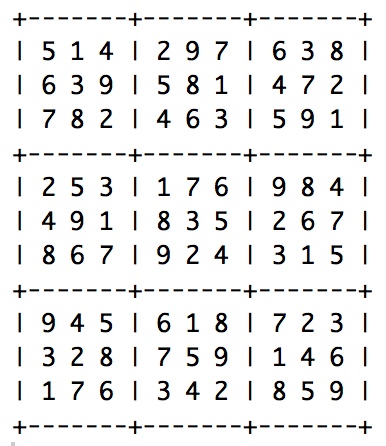
Here are the sudoku solutions used for the other pieces that are played in C and B nine tone scales (the “solemn and adagissimo” is restricted to only two voices, voice 1 and 2):


7. ending, for the slow moon	3. decisive but lento	6. solemn and adagissimo

Pieces 2 and 5 use the E and G nine tone scales, placed on the Michelsonne toy piano as in the following pictures.

E nine tone scale, E(3)-Fis-G-Gis-Ais-B-C-Cis-Ais

G nine tone scale, G(3)-A-Ais-B-Cis-Dis-Es-E-Fis

The following are the sudoku solutions used for the two pieces that are played in E and G nine tone scales:


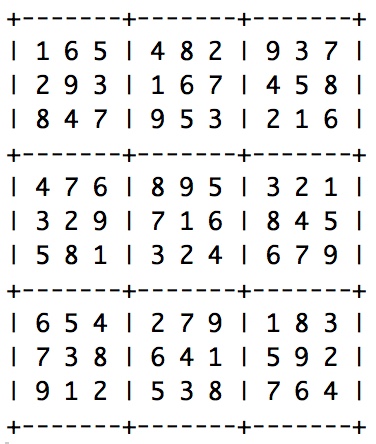2. wavering and adagietto	5. somexwhat hesitant, larghetto

For the recording now available on Bandcamp, each of the the pieces was scripted in Ruby and played by Sonic Pi, using the recorded notes of Emmanual Rébus' Michelsonne toy piano. The four toy piano voices are backed by an electronic voice, also scripted and played by Sonic Pi.

For a live performance, a score of the toy piano voices with additional instructions is available. A such performance will need four players and four Michelsonne or comparable toy piano's. A such performance can be done with just the four toy piano's, and hence limited to the pieces 1, 2, 3 and 5, 6, 7. Or, like in the recording, on might add an improvising electronic voice, preferably performed on a vintage electronic organ.

Here are the first 11 bars of “1. beginning, strict and allegretto”:

On the sequencing of a sudoku solution

Maintaining that something ‘is outside of space time’ must strike you as a blatant contradiction in terms. For, far and deep as our mind's think-string wave vibes reach, is it not that the notion and facts of ‘being‘, surtout that of things, remain inherently tied to that huge and ungraspable stage, of which each of our selfs is the very center (you are the center of the world! ... But so am I :), built from what since time immemorial we call space and time, and what somewhat more recently we have come to ‘see’ as a geometry of four inseparable ‘dimensions’? ‘Outside of this space-time‘ no is can be, can there? The only way to ‘play‘ is within and we are in it. But is space-time really an outside of us, or is it a 'mere' side-effect of our mind's grinding? Sort of like the extension of consciousness, i.e. the complement of its intension.
()
Some speculative philosophysical theories seem to allow for a meaning of ‘being outside space-time’. E.g. given multiple parallel spaces times that accomodate for the continuously branching of our lived and recalled histories, inside one space-time one sort of is outside the others, bundled as in some superstructure, a multiverse, that hosts (the hallucinating number of) all possible worlds.
()
When does a branching occur? At the nanoscale of time, pico, femto, atto, zepto, yocto, ronto, quecto, or all the way down to Planck time and beyond? What, where and when are here the A's in “for all A such that in our world W : Possible(W(A)), there is a world W' such that W'(A): for anything A that at some point in our world's history was a future possibility, there is a world where A will become a recorded part of that world's history (cf. David Lewis' modal realism). ◊W(A)→∃W′(W′(A))◊W(A)→∃W′(W′(A)), all that is possible is bound to happen somewhere:

But apart from that, how about numbers and other platonic stuff? Can these maybe be said to exist, outside space and time?

But let me not stray too far off topic.

27 latin variations on a Sudoku Solution for Perished Piano

« play that piano
inaudible to the world
infinite pleasure »

Unlike the foregoing experiments in sudokism, that for the muzic's generation all used a (small) set of different sudoku solutions, the variations on a sudoku solution for perished piano are all drawn from one single sudoku solution, in casu the seventh in the series of 52 sudoku solutions that I used in 2020 to do the weekly K7 sudoku's.

Back then, these 52 sudoku solutions were chosen pretty much randomly, one a week. Also this time, I had no particular reason for picking this sudoku solution and no other for realising the 27 + 22 pieces for piano. For perished piano. The perished piano that I keep in a garage box not far from my house.

The piano that perished used to be my mother's. It's the instrument on which as a kid she did her Czerny, and the Mozarts, the Beethovens, the Chopins. I saved it from being sold or dumped when she passed away a couple of years ago. The many years it was with her, it lived in post-WWII suburbs of the city of Maastricht. At a number 9. First, pretty much all of the nineteen-sixties years at 9, Micastraat. Then many decades, from the nineteen-seventees onwards, way into the new millennium, at 9, Kurasruwe. That nine (9) then therefore is a sort of random fact that adds to its suitability (predestination?) as a candidate sudokist instrument.

The sequencing for these 27 + 22 variations on one and the same soduko solution here is done in pairs of column-row. For the pitches, a column (in the example right below it is the eight column, c[7]) is read from top to bottom, which then is followed by the reading of the corresponding row (in the picture the eight row, r[7]) from right to left. The numbers are read as intervals in semi-tones, alternately plus and minus, starting from piano key number 48 (of 85). All nine pairs of columns and rows are thus read, which then, in 162 steps brings the sequence of notes back to where it started, to note / key 48 (which, were the instrument in tune, would be a G4).

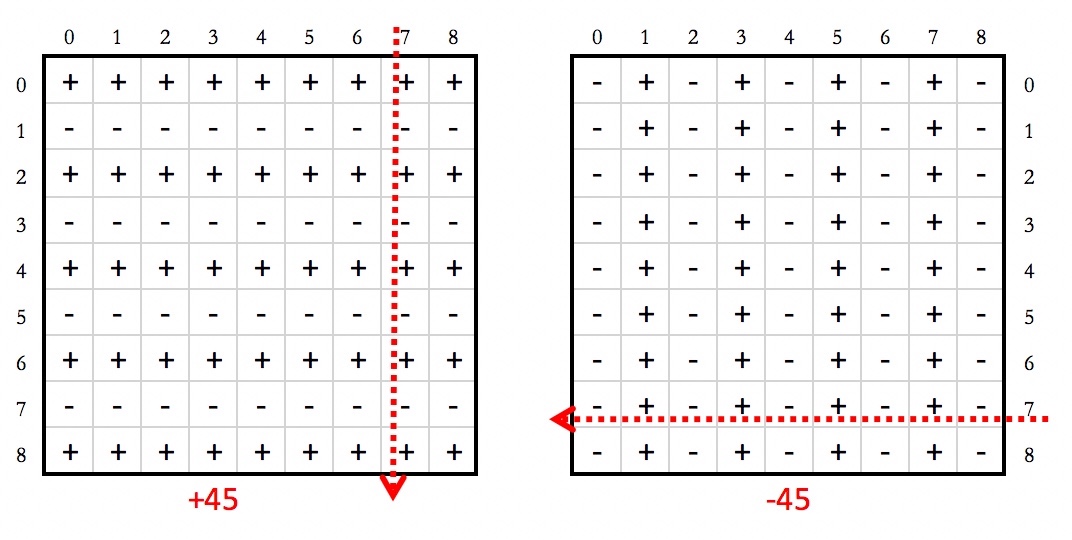
The sequence always will end where it started: this way of sequencing the sudoku solution is cyclic.

The sequence of 162 durations is read off the grid in a similar way, using the same column-row pair, but then read first as a row from left to right, followed by the corresponding column read from bottom to top.

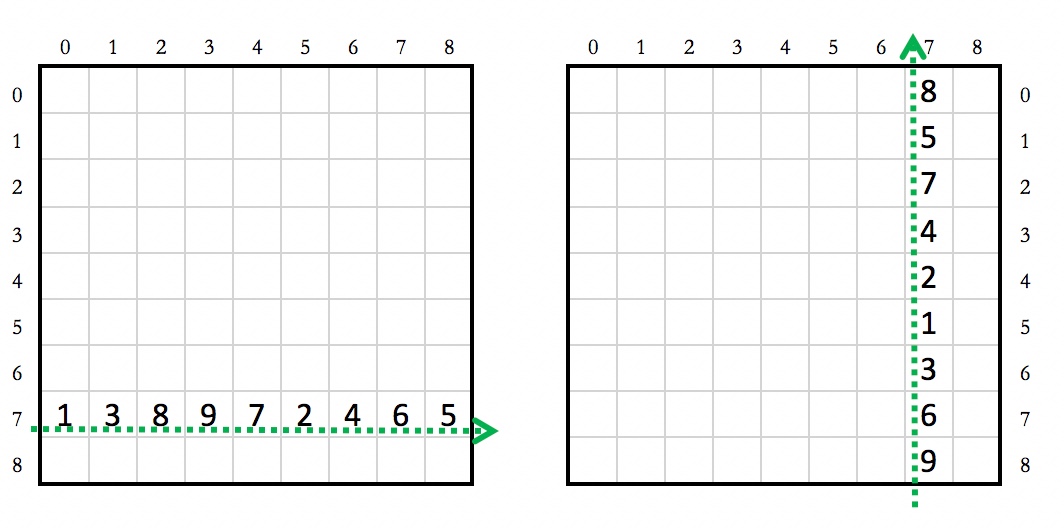
As an example: if the first column / row pair of the above sudoku are used, then the sequencing of the intervals and the corresponding durations will start as follows:
[intervals] 7,-8, 9,-5, 4,-3, 2,-1, 6,-6, 8,-1, 9,-2, 5,-3, 4,-7 ...
[durations] 7, 4, 3, 5, 2, 9, 1, 8, 6, 6, 1, 2, 3, 4, 5, 9, 8, 7 ...

In case this were the beginning of a variation, the sequence of key numbers played by this ‘first voice’ are [48+7=]55 for 7 ticks, [-8=]47 for 4 ticks, [+9=56] for 3 ticks, [-5=]51 for 5 ticks , [+4=]55 for 2 ticks , [-3]52 for 9 ticks, and so on ...

perished piano sudoku sequencing example start voice 1

In each of the variations, the first voice of the piece is determined by this column/row pair sequencing of the sudoku solution, for some given order of the pairs. In the latin variations, the orders used are those provided by the 9-permutations in the sudoky's columns, in the sudoku's rows, and in the sudoku's squares, making for a total of 9+9+9 = 27 variations, which, in the recording are named c[0] to c[1], r[0] to r[8], and s[0] to s[8].

Each of the 27 pieces then comes with a second voice, that is the exact retrograde of the first one.

The 27 pieces are called the 'latin variations' because permuting the sudoku solution will in general not result in another sudoku solution, but merely in a latin square (see earlier post).

The images below are the pitch-duration graphs for each of these 27 latin variations, drawn in R, each with an additional title, that is the permutation of the 9-word phrase “outside of space time is a contradiction in terms” corresponding to the permutation of the order of sudoku solution's column/row pairs that generated the variation's sequencing. E.g. in the first image that permutation is the one given by the sudoku solution's ninth column, (6,2,4,3,9,7,1,5,8), which gives the permuted phrase “a of time space terms contradiction is in".

“a of time space terms contradiction is in"

“in is contradiction time of outside space a terms"

“outside terms space a is in contradiction time of"

“terms space in outside contradiction time a of is"

“of time a terms space is in contradiction outside"

“is contradiction outside of in a time terms space"

“space outside is contradiction a of terms in time"

“time a of in outside terms is space contradiction"

“contradiction in terms is time space of outside a"

...

“contradiction time space outside a in terms of is"

“is of terms space time contradiction outside a in"

“outside in a of is terms space contradiction time"

“is in contradiction a outside time space terms of"

“of terms outside contradiction space in a is time"

“a time space terms of is in outside contradiction"

“of is terms in space outside a contradiction time"

“time in a of contradiction terms space outside is"

“contradiction space outside is a time of terms in"

...

“a contradiction time space outside is of terms in"

“outside space in terms contradiction of time a is"

“of is terms time in a contradiction space outside"

“space terms of a is time in outside contradiction"

“time outside a in space contradiction is of terms"

“is in contradiction of terms outside a time space"

“terms of is outside a in space contradiction time"

“in a outside contradiction time space terms is of"

“contradiction time space is of terms outside in a"

For the realisation of the pieces, I played and recorded separately each of the 85 keys of the perished piano in the garage box, and then scripted, played and recorded the pieces in Sonic Pi. The software actually added its own peculiar performer's flavour to the piece, due to lag occurring in the playing of the two duration sequences. I also interspersed the doubly cyclic sequences of tones by the random hitting of chords and clusters, a bit like having Jackson Pollock splash black or otherwise coloured drops of paint on a Mondrian.

And then there is, of course, the un-tuned- and broken-ness of the old piano, that gives these recording their own, very unique, sad and solipsist, voice. Together this and its companion set of variations, each one generated from the same two-dimensional grid of 9 x 9 = 81 digits, extract a rich sonic and musical universe, fully sufficient onto itself, from a singular, contingent, numerical logic.

22 sudoku variations on a Sudoku Solution for Perished Piano

The 22 sudoku variations on the same sudoku solution form a second set of pieces for the perished piano. This time the variations are generated by mappings of the grid that do preserve the property of being a sudoku solutions.

They consist in the results of the 6 permutations of the three consecutive blocks of three columns:

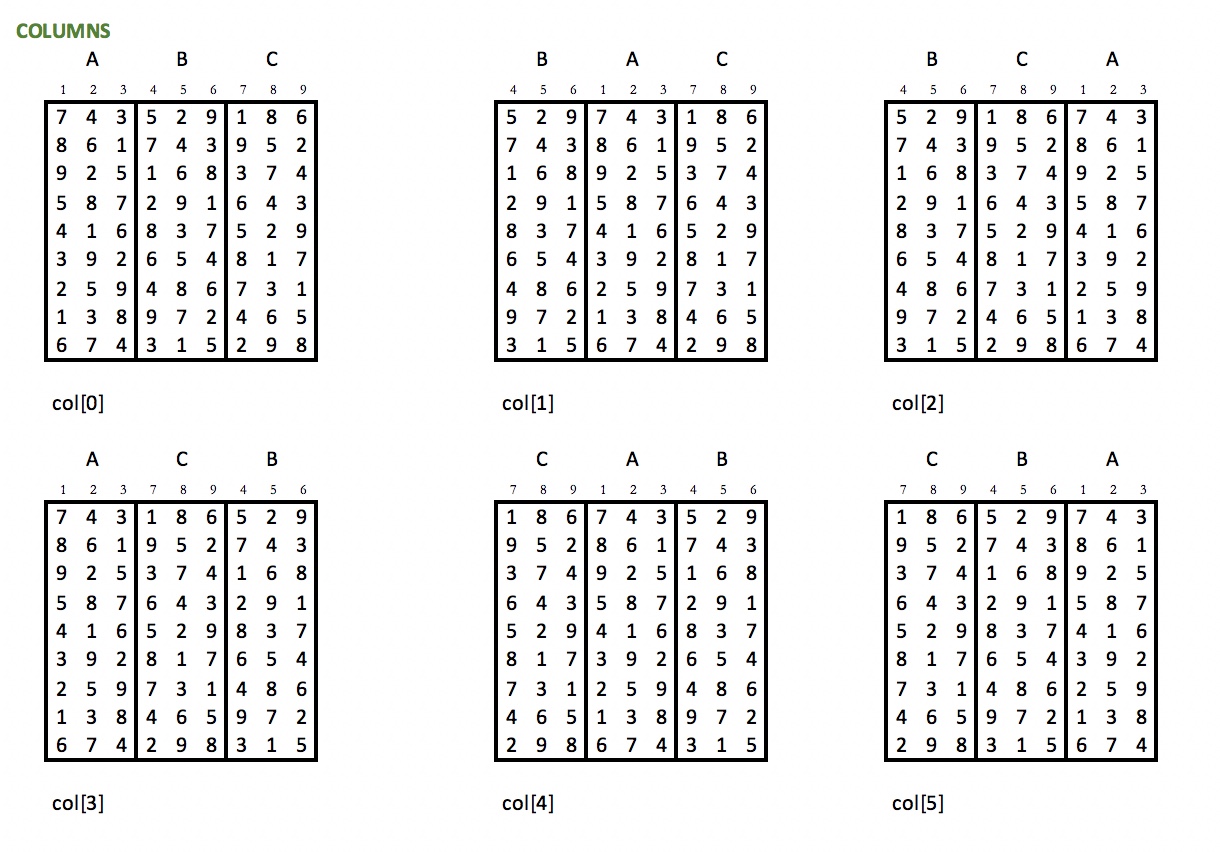
... the results of their 6 transpositions:

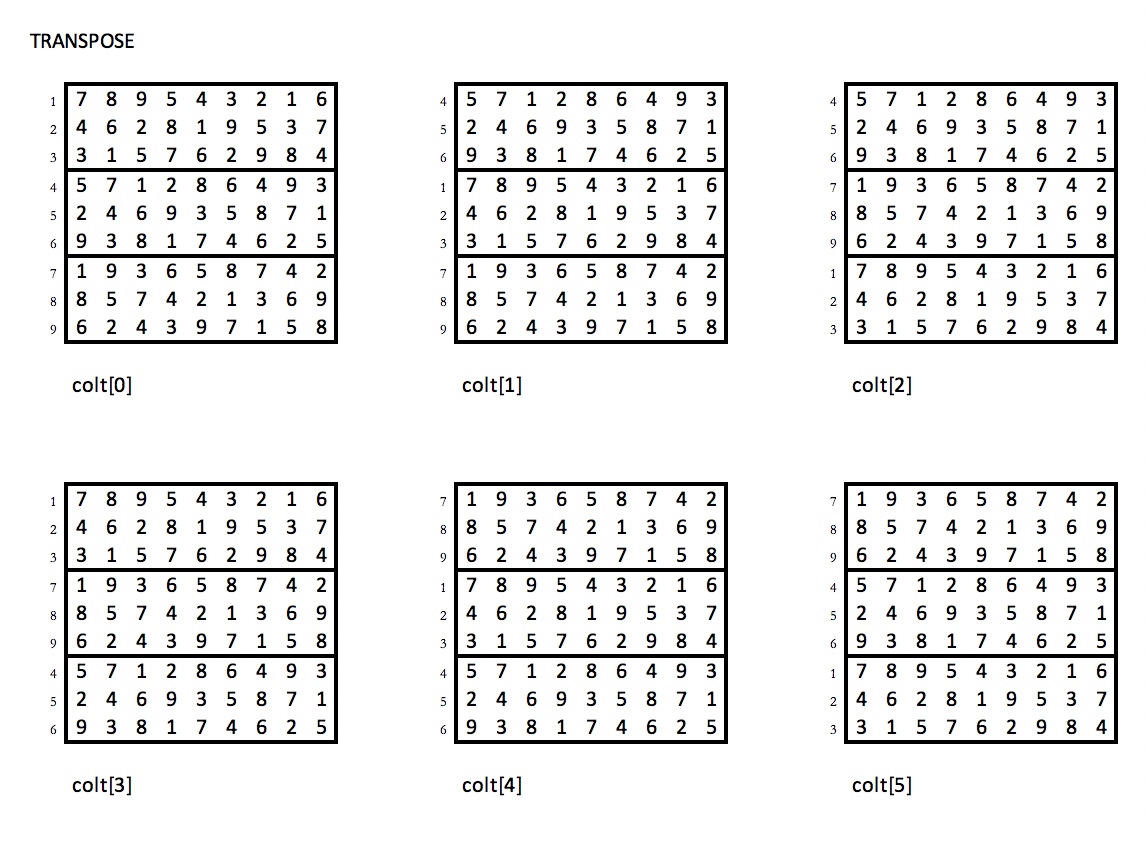
... the results of permutating the three consecutive blocks of three rows:

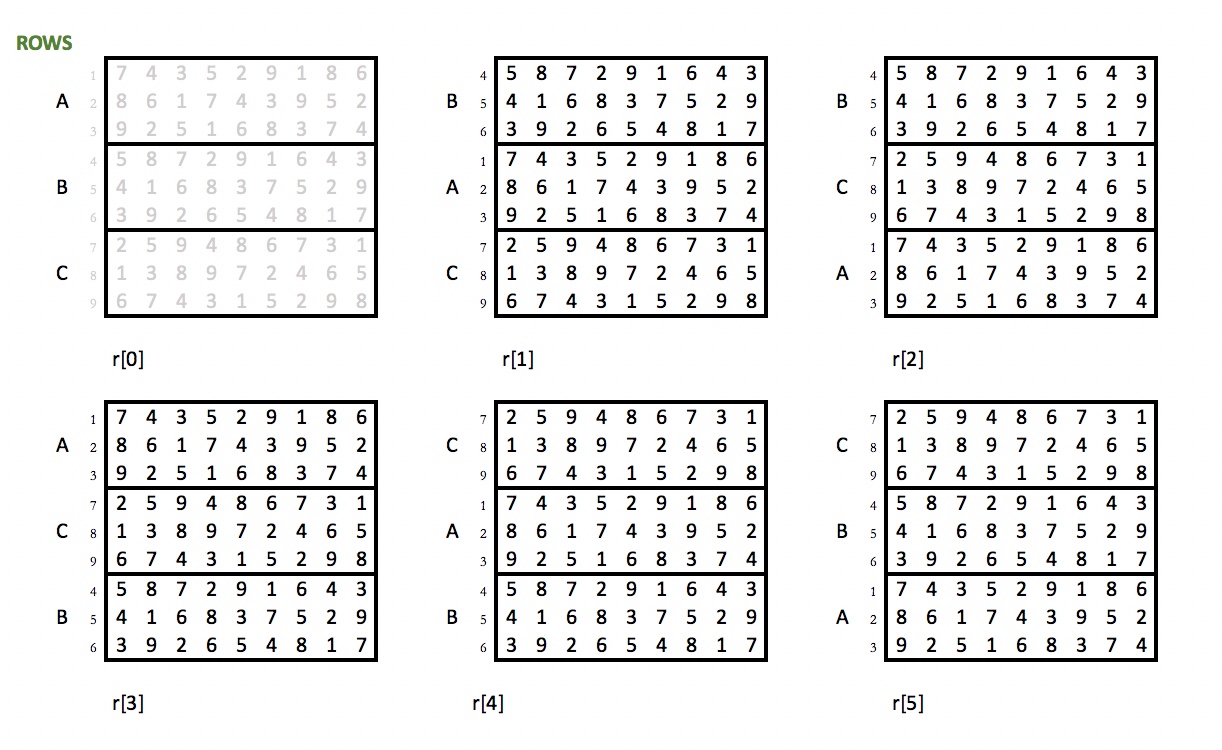
...and then finally the results of their transpositions:

As one sees, the resulting 24 number-grids contain two duplicates (col[0] = r[0], and hence also their transpositions will be equal, colt[0] = rt[0]), which is why the resulting number of variations is 22.

Also for these 22 variations you find the pitch-duration graphs in the images below, drawn in R, and again each with an additional title. In this case, for the cols[i] variations, these titles are 6 the permutation of the trigrams in the 9-word phrase “outside of space time all that is at once” corresponding to the 6 permutations of the three-column blocks that generated the sudoku variations used for the sequencing. The colt[i] titles are the retrogrades of the cols[i]-ones. The permutations of the initial phrase given as additional titles to the r[i] and rt[i] variations, however, are not obviously related to the transformation applied to the sudoku grid; consider them freely improvised.