UPCOMING: June 16-22 2025 ~ (Rotterdam, the Netherlands) :: LIVE in WORM :: HAROLD SCHELLINX Post-Post ULTRA (van 1983 tot en dan almaar verdur) :: (it is all) Politics >:> eternity, unPublic, sudoku's, Commuters, 1024, k7, collage, Gentle Slaughter ... Concert on Saturday, June 21. Drinks on Sunday 22!!
SUBSCRIBE to soundblog_un_public our personal / private old-school email newsletter alternative to the use of FB, X, Insta and other surveilling & exploiting media. Our occasional newsletter brings web links to new and not-so-new thoughts, to releases, concert dates, texts related to projects / works by Har$, the ookoi, other collabs, etc.
7 mins read 🤓
S.I.N : (Numerorum Musica Quae) Se Ipsa Numerat, or a 'Music of Numbers that count themselves'
may 17, 2025
The first half of the text that follows is in Dutch. For the full English text, go to the Medium version of this article.
Fata Morgana
Vorig najaar las ik aandachtig het uitgebreide en eerbiedige boek dat Gilbert Delor wijdde aan het oeuvre van de Amerikaanse componist Tom Johnson, die ik voornamelijk kende van zijn regelmatige bezoekjes aan La Générale Nord-Est, toen die nog aan de avenue Parmentier zat,
niet ver van Johnson's woning in de rue de la Roquette en de keren dat er daar werk van hem werd uitgevoerd, zoals tijdens het feestelijke concert op 18 april 2015, bij gelegenheid van zijn vijfenzeventigste verjaardag, en het enkele kopje thee dat we samen met Magister Rébus thuis bij hem en zijn eega Esther Ferrer nuttigden, waarbij hij ons enthousiast de prachtige diagrammen toonde gebaseerd op de combinatorische en arithmetische principes die hem op dat moment bezighielden, en hij altijd weer polste of wij misschien, als mathematen, hem misschien bij het beantwoorden van de vragen die hem daarbij door het hoofd spookten, konden helpen.
Het (Franstalige) boekwerk van Delor verscheen in 2021, en draagt als ondertitel ‘La Musique Logique’ (de logische muziek). Het werd de aanleiding voor mijn veertigste hoofdstuk in Gonzo (Circus) Magazine, getiteld 'Pakken van hetzelfde laken', dat in de november/december editie van 2024 verscheen. Over Tom Johnson, muziek, getal en logica.
Het extra Gonzo auteursexemplaar dat ik kreeg toegestuurd had ik hem bij de eerste de beste gelegenheid willen overhandigen. Maar nog voordat ik daartoe kwam, overleed Tom Johnson. Op de laatste dag van het jaar 2024. Hij werd 85.
De sfeervol donkere foto hierboven maakte ik op 20 februari 2014, tijdens wat Johnson een 'progress presentation' noemde van zijn 'Counting to Seven'; ook dat gebeurde in La Générale, toen nog aan de avenue Parmentier.
Delors boek ontvouwt in veel technisch detail Tom Jonhnsons levenslange queeste voor een essentie, de graal die hij zocht, een iets dat de kern, het wezen, van ons tellen en getallen (en daarmee van muziek) zou kunnen ont-hullen. Het is het verslag van een speurtocht die—bijna zou ik schrijven: natuurlijk— vergeefs moest blijven. Zo'n kern is als een fata morgana, een spookbeeld: als je er dan na veel gezwoeg vóór staat en hem grijpen wilt, die kern, dan ontglipt hij je weer, en verplaatst zich naar nieuwere en eerder nog onvermoede verten.
Het is geen wetenschap die Johnson in zijn werk bedrijft, alle gecijfer niettegenstaande. Het is puur poëtische speculatie, en de kunst zit 'm in de keuzes die hij daarbij constant maakt. Hoe onontkoombaar die dan misschien ook lijken te zijn. Onder alle eigenschappen en processen van getallen en structuren die Johnson zo gestreng exploiteert is er niet één die niet ook op talloze andere net zo gestrenge manieren anders verklankt zou kunnen worden. Tom geeft ons de verklanking die Johnson koos. En die keuze, die keuzes, dat is hij zelf, de kunstenaar, hoe hij leefde, waar hij leefde, en de wereld waarin hij dat deed. Ha, ha, ja, vandaar dat fata morgana effect!
For an English rendition of the above paragraphs, go to the Medium version of this article.
Zelftellers
Reading Delor's book, especially the parts on Johnson's earlier 'counting' works, brought back memories of a bunch of number 'games' that I pursued in the mid-1980s, in my early 'math' days. One in particular re-caught my attention: the simple recursive recipe that (often, but not always) leads to numbers that, so to say, describe themselves. You will find the mention and descriptions of such numbers or sequences of digits here and there, in a number of variations (more or less similar, but often not quite equivalent), that go under names like 'self-describing sequences', 'self-counting numbers', 'self-describing numbers', 'auto-counters'. I got to know them in Dutch, in the mid-1980s, where they popped up some day in the puzzle section of Folia Civitatis, the weekly news paper of the University of Amsterdam, as—if I remember rightly—'self-counters': 'zelftellers'. In French we might call them nombres auto-referentiels.
Here is a pic of a page from one of my notebooks from those days, on which I wrote down all the zero-less nombres auto-referentiels with a length of between 4 and 18 digits.
There are 58 of them.
There is only one that is smaller, which also is the first evident example of this numeric self-reference. That is the number 22, read as saying: "I am made up of two 2's". Yes, the number 22 describes itself. It is the smallest self-counting number (the smallest 'compact' one, compact—my terminology—meaning that we exclude 0 as a digit that counts :).
Playing around a bit, you will soon find that you stumble on a good many of these auto-counters by picking some number to start with, and then iterate the process of taking its 'descriptor', its 'descripting number'. (For each of the possible 'auto-counters', there of course is a smallest number that generates it. The smallest generator for 22 is 22.)
Here is an example that shows how this works, starting from 123:
123 → 111213 → 411213 → 31121314 → 41122314 → 31221324 → 21322314 → 21322314 → etc ...
And here the process gets stuck in a cycle: we hit a fixed point, a 'zelfteller'. The number that describes 21322314, the descriptor δ(21322314) is 21322314 itself.
(The smallest generator in this case is 1, and it takes 12 steps to find it: δ12(1) = 21322314, see the picture a bit further.)
Recalling these very rhythmically 'expanding while repeating' number patterns caused by the 'digit-counting' operation δ when reading Delor's book, I thought writing them up in a score, that I might one day give to Tom, on a next tea visit, or some other occasion. Because it obviously felt 'Johnsonian', but digit-wise also is firmly rooted in a 9-ness, which linked it to my sudokism, haha. (As for the sudoku's, a fun little fait divers that I picked up from the listing of Tom's 'rejected and occasional works' in the back of Delor's book, is that in the same year that I first used a sudoku solution as a score for dictaphone, in 2006, Tom Johnson did a thing he called 'Sudoku for musiciennes', printed as a business card for the salon Musicora in the Louvre Carrousel.)
I gave my effort a Latin title: '(Numerorum Musica Quae) Se Ipsa Numerat (1)' (which in what follows for brevity abbreviates to S.I.N_1), a Music of Numbers that count themselves (there is a '1', because maybe I will make some more later :). It basically unfolds the digit-count re-writing up to an auto-counter for the nine non-zero digits in counting order (1,2,3,4,5,6,7,8,9), in two parallel voices: the second one does the counting of the digits in their natural counting order, and the first in the order in which the digits are encountered. E.g., '2321' in counting order rewriting becomes '112213', but in appearance order rewriting it leads to '221311', because in 2321 there first occurs a 2, then a 3, and the last digit encountered is a 1.
(If we denote this second operation by γ, then γ(2321)=112213, while δ(2321)=221311.)
The following pics show you almost all the information needed to produce yourself the score for S.I.N_1.
In the first one we see how each of the first four non-zero counting digits 1, 2, 3 and 4 γ-rewrites to a 2-cycle 23322114 ↔ 32232114 (permutations of the δ-zelfteller 21322314), while digit-counting 5 leads to 3322311415, 6 to 3322311416, and so on for 7, 8, and 9, where it ends in the γ-zelfteller 3322311419.
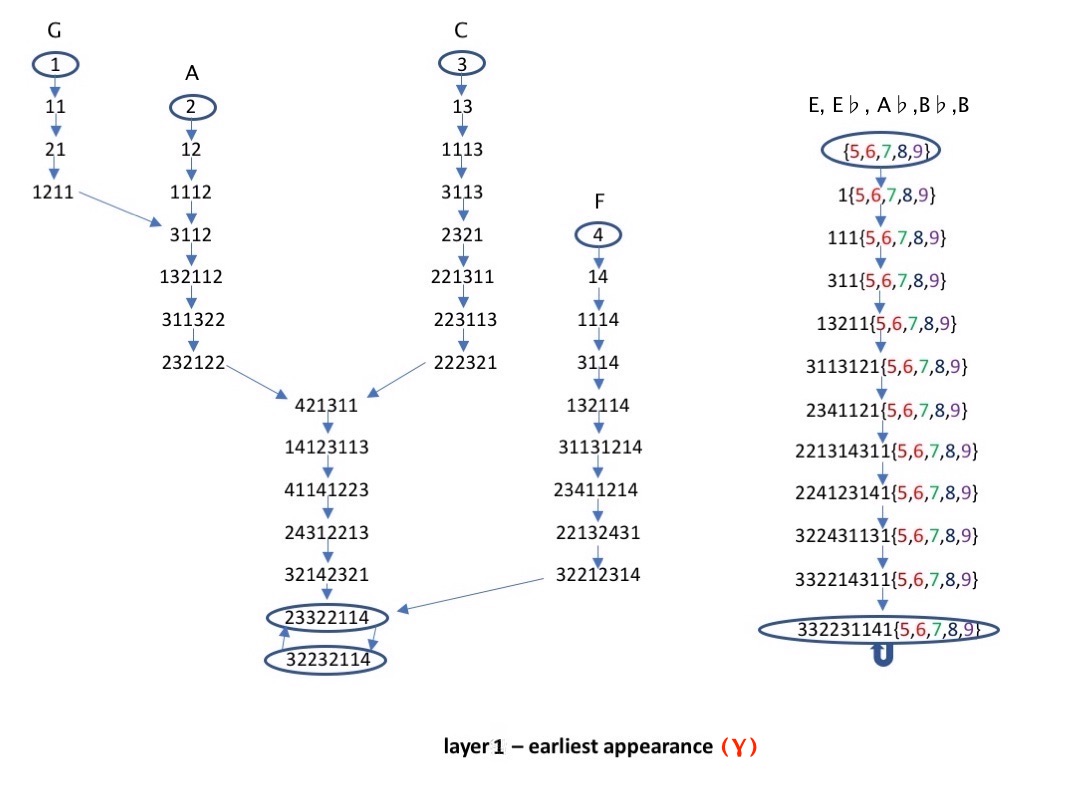
The second one shows how each of the first four non-zero counting digits 1, 2, 3 and 4 δ-rewrites to the auto-counter 21322314, while digit-counting 5 leads to 3122331415, 6 to 3122331416, and so on for 7, 8, and 9 ending with the auto-counter 3122331419.
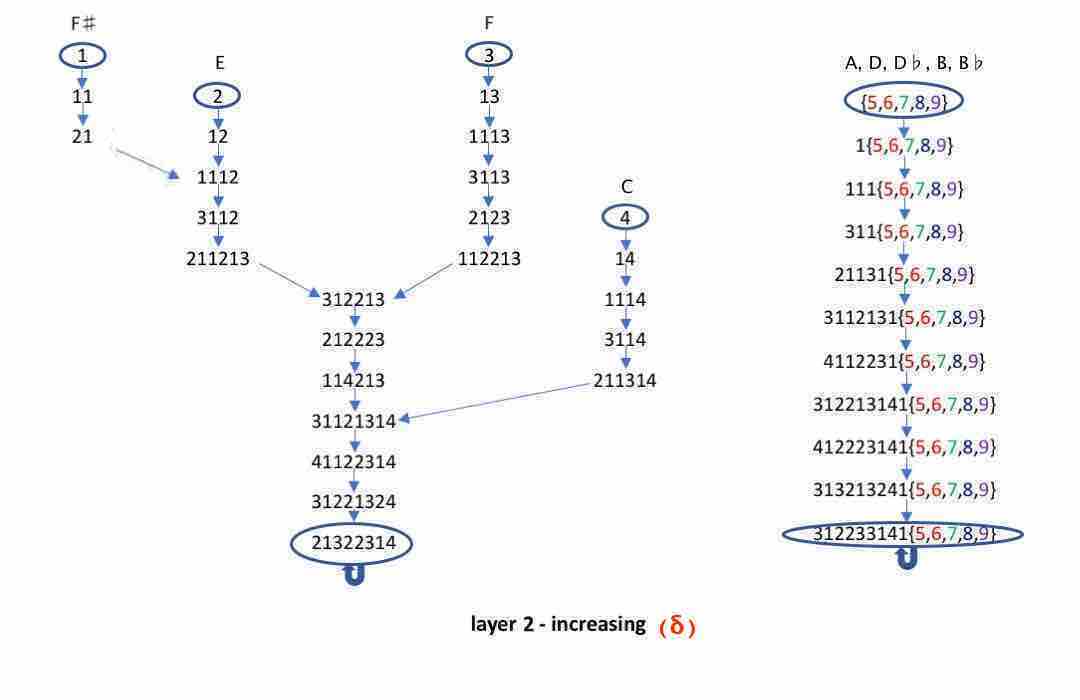
The digits provide the parts of the piece, and for their musical rendering are assigned distinct nine-tone scales (like in the toy piano sudoku's), as indicated in the pictures. Without going into all the details, the first ten measures, annotated with the corresponding numbers will give you the general idea:
For the one-before-final part of the piece I I sneaked in a 'zero', by using 10 as generator, and interpreting the (single) recurring 0 as a rest. The piece then ends with a brief index, a summing up of the auto-counters that are generated in the piece.
One final little fact: when I recently re-checked the numbers, I found that in that one-before-final part, with 10 as its generator, I made a counting error. I decided to not correct the error, and leave it as it is, so that if one day you lay hands on the score, you'll have a chance find it :-)
So, no, unfortunately I will not be able to hand Tom this humble present/hommage. Maybe though one day we can hear it being played. S.I.N can be performed basically by any two instruments, though I really would love to hear it being done by two saxophones, a tenor, say, for the γ-voice, and a baritone for δ ?
One day, maybe.
tags: Tom Johnson, zelftellers, autodescriptive music
# .556.