Curiosity, Cubes & Numbers

december 09, 2012.

"The Answer to Life, the Universe and Everything"

[ sci-fi | curiosity | geeky | cube formulas | postscript ]

Imagine a voluminous Cube, that one sunny morning suddenly comes descending from the heavens. It can be seen hovering high above some large open space (turning very slowly, and swaying, but only a little bit). Let's say all of this is happening in a politically neutral spot, like a couple of miles east of a small Swiss mountain village. Though it would be kind of interesting to just leave it dangling there, at the board of a large, picturesque lake, and have everybody go about their usual business, this is not the sort of thing that in our world will go unnoticed for very long. (Unless, of course, such things actually do go unnoticed, and there's gigantic Cubes floating around us everywhere...) You let a couple of young American hikers spot this particular Cube, and imagine, in pretty much the same breath, a curious crowd of farmers, villagers, school kids, tourists, reporters and local television crews, circling the as yet unidentified object. They're snapping loads of pictures and cell phone clips, that almost instantly give rise to a viral flood on YouCube, Cubebook, InstaCube, TwitCube, and so on. [ Couple of fine panoramic shots and lots of panning, here. ] This been taken care off, you start thinking about the Cube's precise dimensions. You would like to let the initial length of its sides be approximately half of the height of today's tallest building in the world (the Burj Khalifa (برج خليفة‎) in Dubai). Thinking digitally, evident choices will be to have the Cube's sides' length equal 409,6 meters (= 2¹² decimeters), or 409,7 meters (= 2¹² + 1 decimeters). As the thing is held by a couple of cables attached to one of its 8 corners, the effective height of the Swiss Cube will be equal to the length of its diagonal: either √3 × 409,6 ≈ 709,45 meters √3 × 409,7 ≈ 709,62 meters. So you let the distance to the ground of the hovering Cube's lowest corner be some 121 meters, making the distance of its upper corner to the ground equal to, or even a tiny bit more than, the height of Burj Khalifa...

Next. Authorities intervene. Local police secures the area around the object and urges the excitedly babbling onlookers to return to their homes, lock doors and windows, and wait for further news and instructions via the usual news outlets. Given the surreality of the event (which surpasses the tons of living fish that could be seen falling from the skies on the heads of the unsuspecting inhabitants of the fictive village of Barslet - a name that in English translates to bar slut, and indeed is intended as such - in a recent somewhat 'twin peaky-ish' Dutch television series), local authorities are quickly superseded by national authorities, which in turn, mere minutes later, find themselves overruled by a team of un-smiling US special task force agents with shaved heads, chewing gums, suits, earplugs and Ray Ban sun glasses.

By now you're ready to bring in the hi-tech needed for a politico-scientific evaluation the 'situation'. This task is concentrated in a team of American experts. Led by Carter, an unflappable elderly physicist (in whose closet later on you might want to pose a couple of skeletons), almost all of them are (relatively) young men, except, bien sûr, for one (1) (exceptionally) smart, beautiful and (very) young woman.

Early on you dismissed the idea of the Cube being held up in the air through the action of a local anti-gravitational field. Anti-gravity would merely be a burden in the unfolding of the drama, as it would make it near to impossible to keep the physics in the Cube's direct surroundings sort of plausible. That is why you opted for suspension by space tethers. On board of the jet that flies the experts and their equipment over to Switzerland, the girl on the team - her name is Kaylee, but her friends call her Spunky - gives a swirling overview of the history and the ins and the outs of the related concept of a space elevator, dating back as far as 1895, when Russian rocket science pioneer Konstantin Tsiolkovsky, inspired by the Parisian Eiffel tower, imagined a tower that would reach all the way up into space. But space tethers will almost necessarily have to link the Cube to a space craft or station orbiting earth. A Chinese craft? Or a Russian one? The ensuing silence on board of the jet and the close-ups of intense worried expressions on the faces of the experts, make it crystal clear that neither the one, nor the other can be considered a realistic possibility...

Here is a summary of the findings of the experts, and the data they collected, the day after the Cube's sudden appearance. The measurements were done on the ground, below the Cube, and in the air. With a manned helium balloon and from inside the two Navy helicopters the experts investigated all of the Cube's 12 edges, all of its 8 corners, and all 6 of its faces.

- The cables used for the suspension of the Cube were made of an unknown fiber of extreme strength and very low density, Carter said. It was vaguely reminiscent of the polyhydroquinone-diimidazopyridine fiber developed by Doetze Sikkema of the the Dutch chemical firm Akzo Nobel, but further analyses were needed to determine the exact molecular structure, the results of which would not be available before several days.

- They had found that, with a probability of somewhat over 95%, the Cube must be thought of as a solid structure. It appeared to be composed of a great many successive layers, each of which was an assemblage of cubelets with an edge length of exactly 1 decimeter. One of the male experts, who was introduced by Carter as 'John', explained, that if the Cube has an outer length of, say, c cubelets and indeed was a solid structure made up of tiny cubelets down to its very core, the total number of cubelets would be c³ and the total number of cubelets making up its first layer: c³ - (c-2)³, being the total number of cubelets of the original Cube minus the total number of cubelets of the Cube that is left over when the first layer of cubelets is removed (the edge length of the second Cube will be that of 2 cubelets less than the edge length of the initial one). However, the experts had been unable to determine the exact edge length of the Cube, though it had to be equal to either that of 4096 cubelets or that of 4097 cubelets, that is 409,6 or 409,7 meters; the total number of cubelets making up the first layer of the Cube therefore had to be 4096³ - 4094³ = 100.614.152, or 4097³ - 4095³ = 100.663.298.

- If the Cube is solid, Spunky continued, this means that it is made up of 4096³ cubelets or 4097³ cubelets. That is, its cubelet volume, c³, amounts to the staggering figures of 68.719.476.736 or 68.769.820.673 ... Both are about 5 times the 13,75 ± 0,11 billion years that, according to the current best estimate within the Lambda-CDM concordance model, have elapsed since the Big Bang. These also are numbers, she said, that you will surely notice to be remarkably equal to the current net worth in US dollars of the world's richest person, the Mexican business magnate Carlos Slim, but she insisted that this should not lead us to hasty conclusions. You'll find the number 68.719.476.736 if in your family tree you count your ancestors over 36 generations (this should take you back to somewhere around the end of the 9th century), provided, Spunky added with a pretty, devious smile, that all of them were distinct individuals. As a matter of fact, many of them will have been cousins, thus drastically reducing the net number of ancestors in each of our family trees. (Both numbers, by the way, are also equal to about half of what current estimations say must have been the total number of homo sapiens that were ever born on earth.)

- The material that made up the Cube proved even more resistant to the analytic efforts of the experts. The texture of the cubelets in the outer layer of the Cube appeared to be different from that in the inner layers. And this, Carter proceeded in a solemn voice, was indeed most extraordinary. The material of the outer layer can best be thought of as 'sort of like glass, but again of synthetic origin', he declared. In order to investigate the Cube from nearby, Carter and John had gone up in a balloon. It enabled them to determine that a slight beat of a hammer would break an outer layer cubelet. With a metallic sound the handful of cubelets they had hit at, shattered into a myriad of pieces, that subsequently evaporated, disappeared into thin air. The second layer cubelets that were revealed, however, resisted all of their attempts at destruction.

- Spunky had come up with a theory. For now, she said, it remains speculation, but it's all we've got, and it does explain how a fragile outer layer could have survived its descent to earth without notable damage. In fact, she explained, it did not have to survive. The details of the quantum chemistry involved were somewhat vague, but Spunky's theory implied that the molecular structure of the cubelets' texture, together with the precise number of cubelets that make up a layer, somehow encoded its own modification. Her calculations predicted that such a textural modification would occur within each of the layers, once its covering layer had been completely removed.

Much more than this we did not learn on the second day.

Meanwhile, the world's powers that be had temporarily buried their hatchets, and directed their combined attention towards locating the source of the space tethers that held the Cube. The data gathered by military satellites - on the third day - pointed to a spot about halfway between Earth and the Moon, which also was the source of an unusual strong and highly concentrated electromagnetic energy field. But even the most advanced telescopic devices were unable to find evidence of something object-like, a spacecraft or whatever, at that same location.

Some spoke about the opening up of a wormhole, even more evoked a long-awaited divine intervention. They called to prayer and urged mankind to - finally -repent. Most, however, admitted that they did not have a clue...

On the fourth day the New York Times's headline read:

" Answers to Life, the Universe and Everything,
are they Inside the Cube? "

...

It is the utter simplicity (of the concept, not in a technical sense) of veteran video game designer and programmer Peter Molyneux's online 'multiplayer social experiment' that fascinates me. The real Cube of course is not dangling from space tethers near a Swiss mountain lake, as in the wacky sci-fi script above. The real Cube is a program steering a free app - Curiosity. What's Inside the Cube? - that has been available for iThings and Androids since 6 November 2012. According to the Curiosity Wikipedia page, at the day of this writing the app has been downloaded by some 3 million users worldwide. That's about 3 times the number of page views my resplendent fringe blog logged in the full 10 years of its utterly brilliant existence. I mean: that's a mighty big audience...

When you start up the app, after a bit of waiting for connection with one of the 22 Cans servers, on your screen you will see the Cube floating in an empty, non-descript, room, sort of like a modern art gallery's 'white cube'. There's nothing on the walls. There are no windows, there's no door. A tap with your finger on the screen will zoom you in on one of the Cube's sides, and lead you close-up to its current outer layer of cubelets. You can hit these, and shatter them, by tapping the screen with a finger, like Carter and John did with their small silver hammer. With a metallic, high clinking sound effect the shards 'evaporate'. (Click here for an impression of what playing Curiosity sounds like.)

The crux of this rather unorthodox video game is that you're not the only one who's shattering the cubelets. The numbers given above were derived from the statistics provided within the app (which, together with the Curiosity stats page at 22Cans's, for now are the only reliable ones that I'm aware of), and correspond to the numbers of the 'real' Cube (more to come, below). The only feasible way to remove all of them cubelets layer by layer, is to have many thousands of users cooperate, tapping away cubelets on their touch screens continuously and simultaneously. At the moment of this writing, a month after the app became available, the world's collective cubelet tapping managed to remove 85 of the 2048 possible layers. That makes a total of 8.206.169.960 cubelets... or maybe rather of 8.210.261.690 cubelets? ... or something in between? (I'll be getting back to these questions a bit later, in the really geeky part :-)

But whatever the precise number: what makes you, me, them do this? And why, 85 layers and more than 8 billion cubelets later, are we still doing it?

First of all, it looks good on your smart phone or tablet. Especially on the iPad it is - at least for a little while - fun and sort of relaxing to sit and tap away hundreds, thousands and more cubelets, that, one after the other or in bunches, depending on your tapping technique, with a clinking sound disappear from your screen, and little by little reveal (at least the color of) that what is below. It surely is the musician in me that makes me do this rhythmically, playing along to the slow synth melody that serves as Curiosity's sound track. But, then after a while (and by now rather sooner than later), that music starts to get on my nerves. And I stop. Until hours, or sometimes days, later I start up the app again, curious to find what the Cube has become.

I'm not much of a gamer (at least not in the usual sense), and probably therefore not very sensitive to such encouragements, but I guess a lot of users will also sort of get 'addicted' to hitting the Cube because of the traditional game mechanisms that are built into it. Smashing cubelets earns you coins, there's a system of bonuses and you can make combo's that will get you even more coins. You can use your coins to buy tools (the more expensive, the more powerful) that allow you, for a short while, to mass destruct cubelets.

The Cube looks different all the time. (Actually, at the moment of this writing, the one on my iPad does not present the same image as the one on my iPhone, though the 'cubelet removal patterns' on both correspond, see pictures above.) Obviously, the Cube's six faces are amazing canvases, and 22Cans are well aware of their potential for getting things across. So, over the past month, there's not only been mono-colored Cubes, Cubes wrapped in images, or Cubes covered with text (from e.g. Lewis Carroll's Through the Looking Glass or Dickens's A Tale of Two Cities). The Cube has also extensively been used by 22Cans to advertise, most notably for a Kickstarter Campaign (via which they hope to raise the sum of £450.000 for their upcoming Godus project). A couple of the Cubes then were covered with the names of backers, in different sizes, probably related to the amount of their pledge.

Far more interesting, though, is the fact that the Cube also provides a canvas to its users, be it an extremely volatile one. The many millions of cubelets on each of its faces not only serve as the pixels that make up the images put on there by 22Cans. Clicking them away allows you to draw pictures, write messages and produce all sorts of graffiti and pixel art, that will remain visible (depending on their size) from some level of zoom, until - either on purpose or by accident - other users make them disappear. I for one quite enjoy roaming the Cube searching for these images and messages (does feel a bit like visiting another planet, looking for signs of intelligent - just a matter of speaking ;) - life).

A couple of game blogs follow the Cube's development on a near to daily basis (here, for example, and here), but there does not seem to be much of a coherent idea behind its continually changing appearance, and as far as I am concerned, there's no longer much of a surprise there. Apart, of course, that you'll never know what will come next :-)

Then, finally, there maybe (still) is the intended curiosity: wanting to find out what's inside the Cube. Its designer, Peter Molyneux, did promise something like a pot of gold at the end of the rainbow. It is not at all clear, and maybe even not yet decided, at which stage, with the removal of which layer, the game will come to a grinding halt. But when that day, hour, minute, second, millisecond, arrives, one - and only one - of the then active apps will be linked to the timestamp of the shattering of the last remaining cubelet. Hundreds of thousands, maybe millions, of users will have toiled for months to peel the Cube, in order to enable one among their peers to find out what's inside. That is another great idea. The winning user's app will automatically receive a link to a video that unveils the Cube's secret, claimed to be "life-changingly amazing by any definition". It will be up to that single user to decide whether to keep the 'secret' for herself, or make it public. (The rules of the game, however, forbid the winner to, in some way or other, use her knowledge for financial gain.)

As things are looking now, hitting upon that final cubelet will be purely a matter of chance. For those using the app at that moment in time, however, the odds do not look too bad. Based on data from the app's release up until the 29th of November, the Curiosity stats page gives a peak user count of 11.000 (and a peak cubelet destruction rate of 18.000 per second). Unless some indication will be given that the Cube's end is near, I think that with the passing of time user activity on the Cube will not get much higher than this. Which would give you a chance of 1 in some 10.000 or less to become the one to shatter the last remaining cubelet. It was indeed just a matter of being active at the right time, that on two occasions my iPad app threw me a 'layer cleared' bonus of 2000 coins, though I doubt this actually means that my app was linked to the timestamp of the destruction of the last remaining cubelet on that layer. I suppose this bonus is given to a whole bunch of users clicking around at the time a layer is cleared.

The clearing of a layer leads to some pretty confusing minutes in the app, with a series of successive (server?) re-settings, during which it is not very cleary whether there actually is a playable Cube. Also the in-app stats stay behind. The screen states 'layer cleared', but the stats continue to show a pretty decent number of cubelets still remaining. At some point actually the number even went up again... But well, technically, running such a massive multi-player platform is sure to be a highly complex affair. Which probably also accounts for the fact that clearing a layer does not really reveal the next Cube. The layer of cubelets that gradually is uncovered on your screen, is of the same dimensions as the current outer layer. Consequently, what you see happening on your screen is not a peeling. The Curiosity program simulates the Cube as six functionally independent faces, which after the clearing of an outer layer are just being replaced, by six smaller ones.

So the real Cube is but an approximation of the theoretical one, be it a pretty neat one. And the theory... well, that's just the 'theory'. Not something that could or would prevent Peter Molyneux and the folks at 22Cans to change rules as they go along, I guess.

Which then finally brings me to the geekiest part of my discours.

This lengthy article actually came about because some weeks ago, quite accidentally, I saw some of the numbers involved being discussed by the editors of the Cube's Wikipedia page. I was surprised by their finding that the edge length of the initial Cube was an even number: 4096. It was not a mere guess on their part, but backed by the screenshot below, which shows the Android in-app stats at some point during the removal of the second layer. Adding the number of cubelets remaining on that day's current (the second) layer to the total number of cubelets destroyed, gives 201.130.048 as the sum of number of cubelets of the Cube's first two layers, which indeed is the number of cubelets that make up the first two layers of a Cube with an initial edge length of 4096.

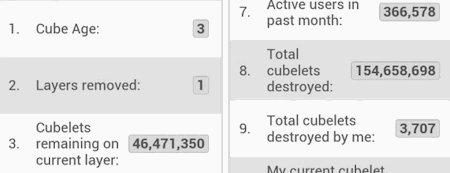
Until then I had taken it for granted that the initial edge length was an uneven number: for only in that case the full dismantling of the Cube will eventually lead to one, single remaining cubelet, a 1 x 1 Cube. If the initial edge length is even, the dismantling will result in a 2 x 2 Cube, identical to the final outer layer, the removal of which results in a void. There would be nothing left. Very quickly, though, I began to really like this idea. For what could be more gratifying then the fact that, ultimately, there's nothing inside the Cube?

Around that same time one of the editors/contributors to the Cube's Wikipedia page started to do some calculations. He added some formulas that would allow you to determine the numbers of cubelets in the successive layers etc., all starting from this even initial edge length. His algebra was overly complicated. It really is little more than trivial counting, so I helped him out a bit, smoothing and simplifying some of his 'math'. However, in true Wikipedia style, other editors (and not unjustly so) considered this 'Cube math' to be out of place, so the math section was commented out. Then put back in again ("I was looking for this information!" one of the undo-ers added as the reason for his undo), commented out again, put back in... and so on. Yesterday it was out. This morning, I just noticed, someone had put it back in again. Bref. It became somewhat of a flasher, which is why I decided to put all of it, in my own way, here on the SoundBlog, if only to be able to easily reference it myself.

It led me to a curious discovery.

In between working on this article in the evening of Sunday December 9th, I was playing around a bit with the iPad app, and by chance I was doing this around the time that the 85th layer was on the verge of being cleared. So I decided, just for fun, to use the in-app stats shortly after the appearance of the next Cube in order to verify that the number of cubelets on the 86th layer was indeed the number 'predicted' by the formulas: 92.433.752. Here is the screenshot that I made of my iPad's in-app stats, mere seconds after the new Cube and the 86th layer had become available in the app:

Disregard the Dutch spelling error. What you need to be looking at is the third number: 92.480.856. That's close to 92.433.752. But close is not enough. I would not have thought twice about this, had it been slightly less than the predicted number. That would have been due to a number of cubelets on the fresh layer already having been clicked away. But how could it possibly be more? The formulas are dead right, trust me. If 85 layers are removed from an initial even Cube, with edge length 4096, then the number of cubelets remaining on the 86th layer is 92.433.752. Not one less, not one more.

Being an expert, of course I have an explanation for this discrepancy. It's a surprising one. And - unless 22Cans's servers are seriously messing things up - it's more than just a theory, Spunky! As a matter of fact, the number of cubelets available on the 86th layer, as shown in yesterday's screenshot, corresponds dead on to the number of cubelets on the 86th layer of an uneven Cube, with an initial edge length of 4097. That number is 92.480.858. I'm pretty confident that the two cubelets less in the stats can safely be accounted for by two cubelets that already disappeared from the new layer at the moment I tapped the stats button.

This, girls and boys, proves without a shadow of a doubt, that even though we have clearcut evidence that, on the 3^rd day of its existence, we all were tapping at the remnants of a Cube with an initial edge length of 4096 cubelets, on the 34^th day we were just as surely all staring at what would have remained if the Cube had had an initial edge length of 4097...

Did Peter Molyneux change his mind? Was the original initial edge length, and an initial Cube with 'nothing' inside, a mistake? Where along the line did the even Cube become an uneven one? Or is it continuously, maybe even randomly, switching between its even and its uneven states, between the 0 and the 1?

Now that would be truly amazing.

It would make the Cube into a Quantum Cube :-) ...

...

[ All of the questions and speculations above of course have definite answers. Just ask Peter Molyneux, or the good people at 22Cans. They're the Cube Gods, and they can do to it whatever they want. But asking (and maybe even getting answers), of course, would make our little game of deduction and, generally, playing at being the experts, a lot less fun. I like the Cube. And I love the theoretical Cubes. Especially the even one. I want it to be stripped down to the very end, where there's nothing left inside, where it simply disappears, without leaving a trace. Without bringing us new answers. Not to Life, not to the Universe, not to Anything. In its profound nothingness, 42 will continue to do just fine. It's a perfect match for the void inside the even Cube... ;-) ]

[ The real treasure of this whole experience, of course, is the incredible amount of data that 22Cans are gathering while the thing unfolds. I cannot but hope that all of it is being kept, complete and unabridged, which would, just to give an obvious example, make it possible to create a time-lapsed re-play of the whole process of the Cube's dismantling, which is sure to make for a truly stunning visual. And in my guise of creator and composer of unusual musics, wouldn't I just love to get my hand on these data and use them in the making of some sort of a score ... (hint :). OK. That's all. ]

...

Overview of Cube Formulas

1. As with the destruction of each layer the length of the Cube's edges decreases by 2, and the initial Cube has an edge length of 4096 or 4097, the Cube will have at most 4096/2 + 1 = 2049 successive layers. Cube_n (the n-th in the series of 2049 Cubes) thus gets edge length:
∙   e_n = 4096 - 2(n - 1) = 4098 - 2n in the even initial case;
∙   e_n = 4097 - 2(n - 1) = 4099 - 2n in the uneven initial case.
(For n you may substitute any number from 1 to 2049.)
In general, given a Cube with initial edge length E = e₁, one finds:
∙   e_n = E + 2 - 2n, for 1 ≤ n ≤ floor(E/2) + 1.
2. The edge length decreases linearly. In the even initial case, Cube₂₀₄₈ is the final real Cube, the last one with a positive edge length: 2. Its successor, Cube₂₀₄₉ , is the zero-Cube, with edge length 0, zero, nill, nada, nothing... In the uneven initial case, Cube₂₀₄₈ will have edge length 3 (like the classic Rubik's Cube): the final Cube₂₀₄₉ will be a single cubelet. (These, of course will also be the final stages for any other even or uneven intital Cube.)
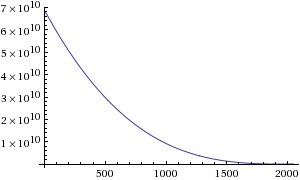
3. The number of cubelets, c_n , that make up the volume of Cube_n, is equal to the cube of Cube_n's edge length:
∙   c_n = e_n³ = (4098 - 2n)³ in the even initial case;
∙   c_n = e_n³ = (4099 - 2n)³ in the uneven initial case.
(Also here, for n you may substitute any number from 1 to 2049.)
The following graph shows the cubic decrease of the sizes of the successive Cubes:



In general, given a Cube with initial edge length E, one finds:
∙   c_n = e_n³ = (E + 2 - 2n)³, for 1 ≤ n ≤ floor(E/2) + 1.
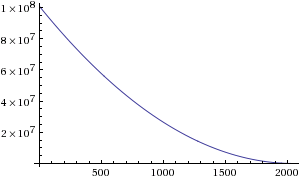
4. The zero-Cube has no layers. So in the even initial case, we put l₂₀₄₉ = 0. In the uneven initital case, l₂₀₄₉ = 1. Each of the preceding 2048 layers is composed of l_n cubelets, and:
∙   l_n = c_n - c_n+1 = e_n³ - e_n+1³ = 6(2n - 4097)² + 2 in the even initital case;
∙   l_n = c_n - c_n+1 = e_n³ - e_n+1³ = 6(2n - 4098)² + 2 in the uneven initital case.
(In these formulas, for n you may only substitute numbers from 1 to 2048.)
The following graph shows the quadratic decrease of the numbers of cubelets per layer:



In general, given a Cube with initial edge length E > 1, one finds:
∙   l_n = e_n³ - e_n+1³ = 6(2n - E - 1)² + 2, for 1 ≤ n ≤ floor(E/2).
5. Finally, you might be interested in knowing the number of cubelets that have been destroyed when reaching the n-th layer. That number - let's call it d_n - will be the difference between the original number of cubelets and the number of cubelets that make up the remaining cube: d_n = c₁ - c_n .

Postscript (added June 15th, 2013)

As was to be expected, 22Cans put an end to the game long before all of the two thousand and something possible layers of cubelets had been clicked away. On May 1st, 2013, the Guilford videogame masters announced that from then, reaching the cube's inside would only take the removal of just 50 more layers, making the cube disappear with only about some 16% of its theoretical number of skins pealed off.

These final 50 layers have taken a little less than a month to complete. The last cubelet was hit on Sunday May 26th by a youngster named Bryan Henderson from Edinburgh, Scotland. Bryan became the first to find out what was inside the cube, and decided to share his 'discovery' with the world. So, what was inside the cube?

In hindsight, we should have known all along.
Inside the cube, there was Peter Molyneux... ;-)

Joking apart: given the gaming context, Bryan did get something rather interesting. Potentially interesting. Let's say: something promising... Still, somewhat sad that, after all, the cube went down so quickly, and did only partly live up to its original 'promise of purity'. I'm mighty glad though that it was not me that hit the final cubelet. I'd rather not become a future Godus God...

Tweet this

Subscribe

tags: Curiosity, game, iPhone, iPad, app, 22Cans

# .431.

comments for Curiosity, Cubes & Numbers ::

Comments are disabled